Venc Design and Velocity Estimation for Phase Contrast MRI

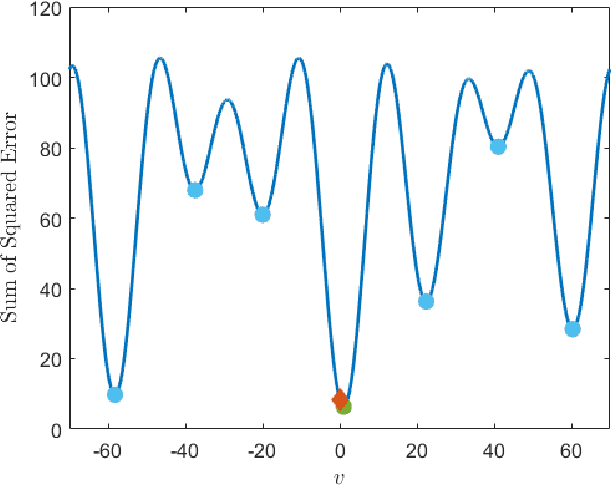
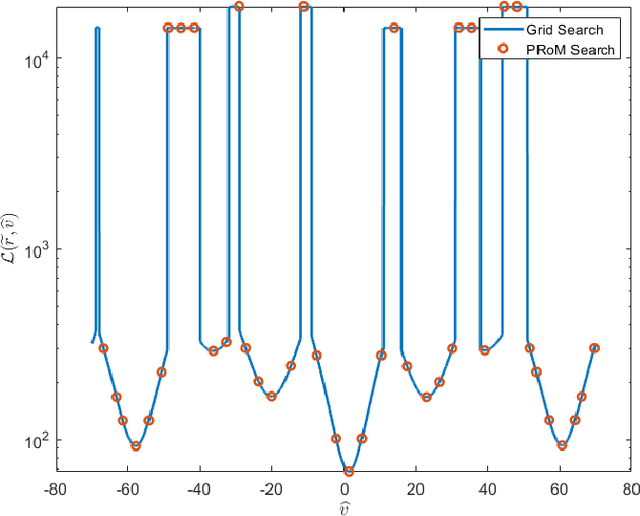
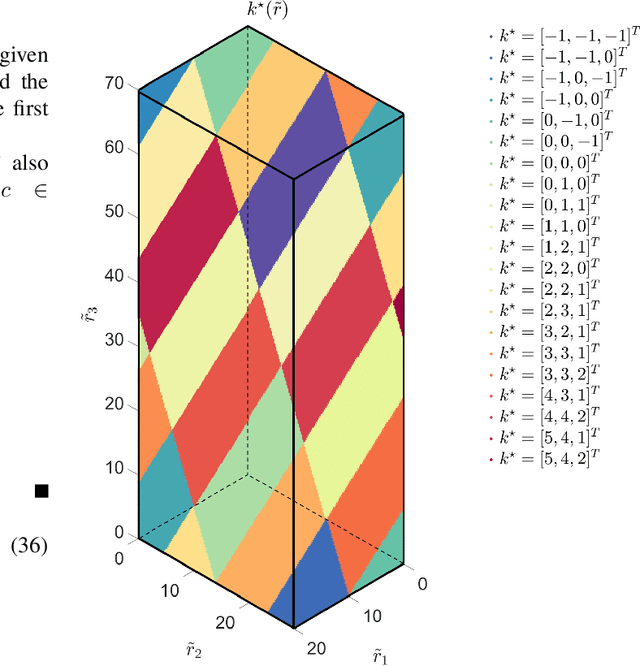
In phase-contrast magnetic resonance imaging (PC-MRI), the velocity of spins at a voxel is encoded in the image phase. The strength of the velocity encoding (venc) gradient offers a trade-off between the velocity-to-noise ratio (VNR) and the extent of phase aliasing. In the three-point encoding employed in traditional dual-venc acquisition, two velocity-encoded acquisitions are acquired along with a third velocity-compensated measurement; their phase differences result in an unaliased high-venc measurement used to unwrap the less noisy low-venc measurement. Alternatively, the velocity may be more accurately estimated by jointly processing all three potentially wrapped phase differences. We present a fast, grid-free approximate maximum likelihood estimator, Phase Recovery from Multiple Wrapped Measurements (PRoM), for solving a noisy set of congruence equations with correlated noise. PRoM is applied to three-point acquisition for estimating velocity. The proposed approach can significantly expand the range of correctly unwrapped velocities compared to the traditional dual-venc method, while also providing improvement in velocity-to-noise ratio. Moreover, its closed-form expressions for the probability distribution of the estimated velocity enable the optimized design of acquisition.