Vector Quantization as Sparse Least Square Optimization
Paper and Code
Sep 24, 2018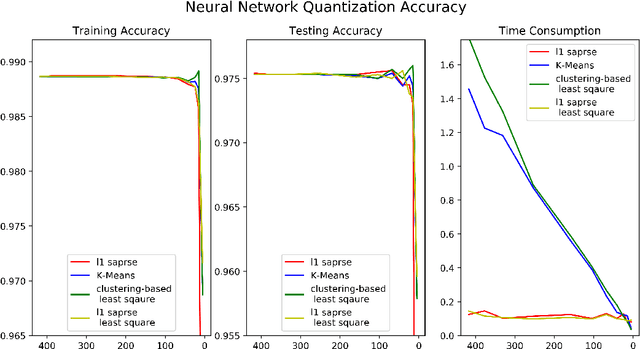
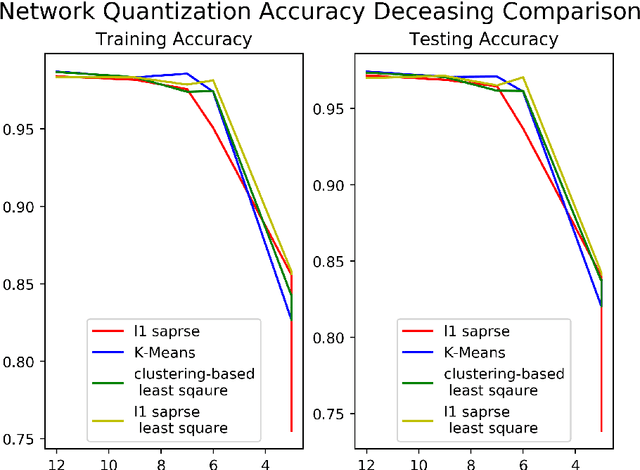
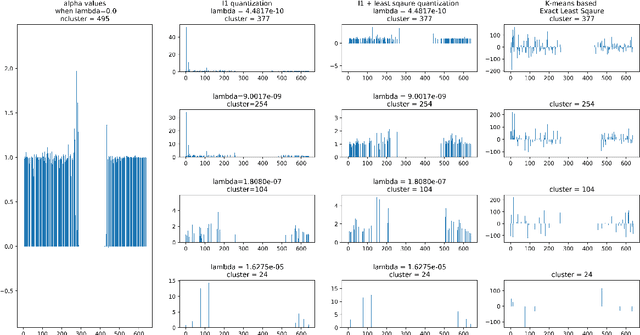
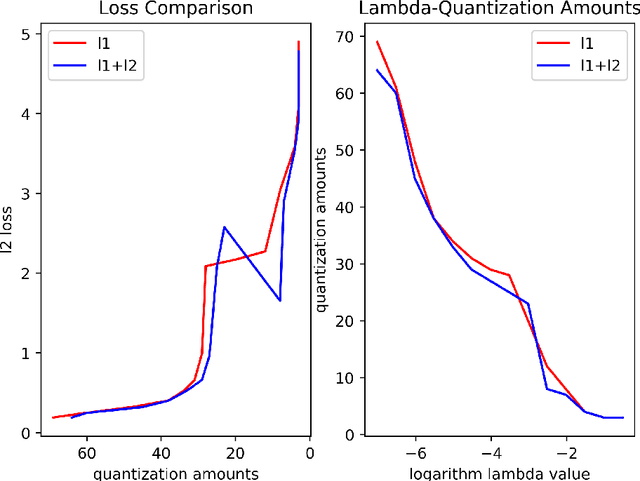
Vector quantization aims to form new vectors/matrices with shared values close to the original. It could compress data with acceptable information loss and could be of great usefulness in areas like Image Processing, Pattern Recognition, and Machine Learning. In this paper, the problem of vector quantization is examined from a new perspective, namely sparse least square optimization. Specifically, inspired by the property of sparsity of Lasso, a novel quantization algorithm based on $l_1$ least square is proposed and implemented. Similar schemes with $l_1 + l_2$ combination penalization and $l_0$ regularization are simultaneously proposed. In addition, to produce quantization results with given amount of quantized values(instead of penalization coefficient $\lambda$), this paper proposed an iterative sparse least square method and a cluster-based least square quantization method. It is also noticed that the later method is mathematically equivalent to an improved version of the existed clustering-based quantization algorithm, although the two algorithms originated from different intuitions. The algorithms proposed were tested under three scenarios of data and their computational performance, including information loss, time consumption and the distribution of the value of sparse vectors were compared and analyzed. The paper offers a new perspective to probe the area of vector quantization, and the algorithms proposed could offer better performance especially when the required post-quantization value amounts are not on a tiny scale.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge