Vector Field k-Means: Clustering Trajectories by Fitting Multiple Vector Fields
Paper and Code
Aug 31, 2012

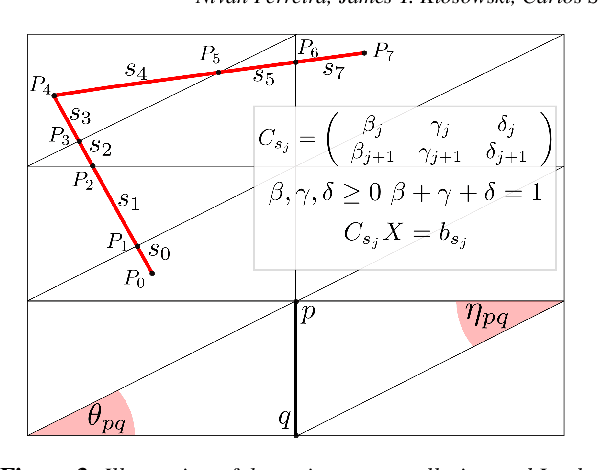
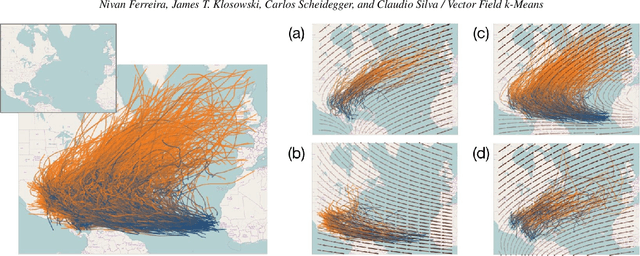
Scientists study trajectory data to understand trends in movement patterns, such as human mobility for traffic analysis and urban planning. There is a pressing need for scalable and efficient techniques for analyzing this data and discovering the underlying patterns. In this paper, we introduce a novel technique which we call vector-field $k$-means. The central idea of our approach is to use vector fields to induce a similarity notion between trajectories. Other clustering algorithms seek a representative trajectory that best describes each cluster, much like $k$-means identifies a representative "center" for each cluster. Vector-field $k$-means, on the other hand, recognizes that in all but the simplest examples, no single trajectory adequately describes a cluster. Our approach is based on the premise that movement trends in trajectory data can be modeled as flows within multiple vector fields, and the vector field itself is what defines each of the clusters. We also show how vector-field $k$-means connects techniques for scalar field design on meshes and $k$-means clustering. We present an algorithm that finds a locally optimal clustering of trajectories into vector fields, and demonstrate how vector-field $k$-means can be used to mine patterns from trajectory data. We present experimental evidence of its effectiveness and efficiency using several datasets, including historical hurricane data, GPS tracks of people and vehicles, and anonymous call records from a large phone company. We compare our results to previous trajectory clustering techniques, and find that our algorithm performs faster in practice than the current state-of-the-art in trajectory clustering, in some examples by a large margin.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge