Variational Optimization for Quantum Problems using Deep Generative Networks
Paper and Code
Apr 28, 2024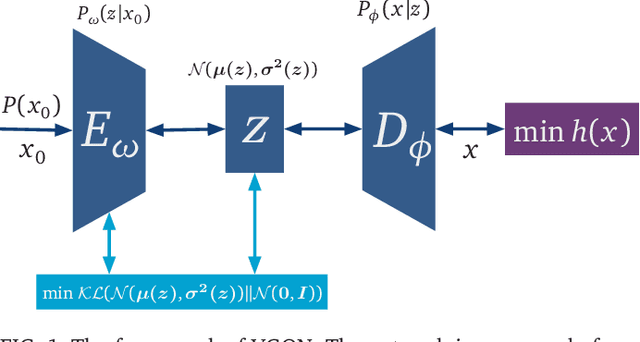
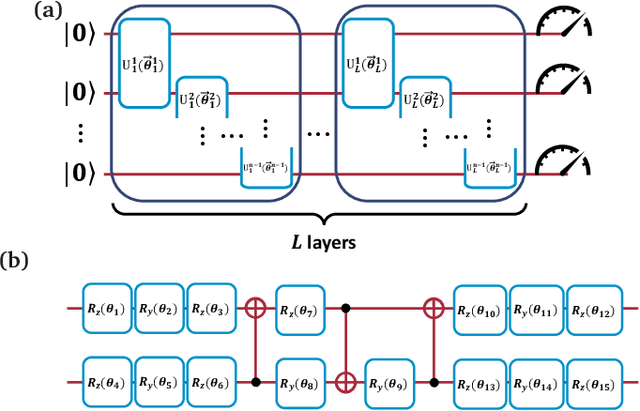
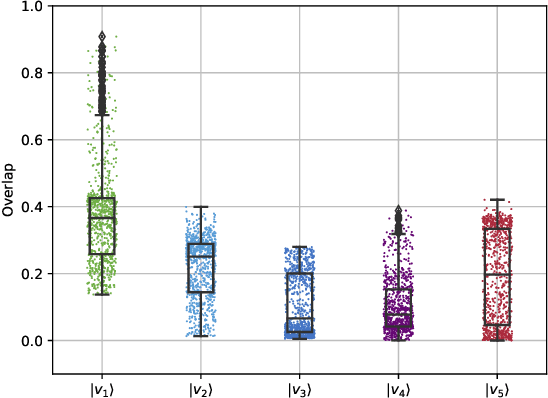
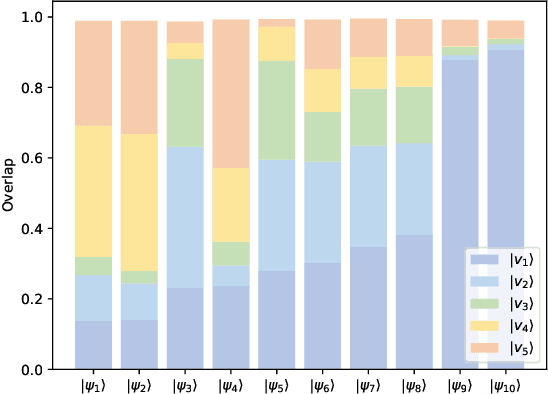
Optimization is one of the keystones of modern science and engineering. Its applications in quantum technology and machine learning helped nurture variational quantum algorithms and generative AI respectively. We propose a general approach to design variational optimization algorithms based on generative models: the Variational Generative Optimization Network (VGON). To demonstrate its broad applicability, we apply VGON to three quantum tasks: finding the best state in an entanglement-detection protocol, finding the ground state of a 1D quantum spin model with variational quantum circuits, and generating degenerate ground states of many-body quantum Hamiltonians. For the first task, VGON greatly reduces the optimization time compared to stochastic gradient descent while generating nearly optimal quantum states. For the second task, VGON alleviates the barren plateau problem in variational quantum circuits. For the final task, VGON can identify the degenerate ground state spaces after a single stage of training and generate a variety of states therein.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge