Variance Reduced Halpern Iteration for Finite-Sum Monotone Inclusions
Paper and Code
Oct 04, 2023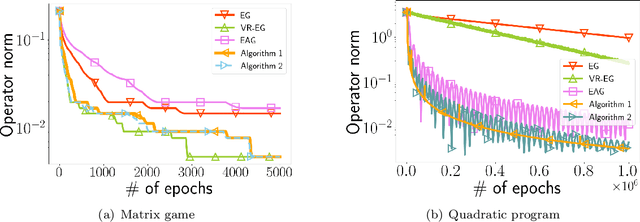
Machine learning approaches relying on such criteria as adversarial robustness or multi-agent settings have raised the need for solving game-theoretic equilibrium problems. Of particular relevance to these applications are methods targeting finite-sum structure, which generically arises in empirical variants of learning problems in these contexts. Further, methods with computable approximation errors are highly desirable, as they provide verifiable exit criteria. Motivated by these applications, we study finite-sum monotone inclusion problems, which model broad classes of equilibrium problems. Our main contributions are variants of the classical Halpern iteration that employ variance reduction to obtain improved complexity guarantees in which $n$ component operators in the finite sum are ``on average'' either cocoercive or Lipschitz continuous and monotone, with parameter $L$. The resulting oracle complexity of our methods, which provide guarantees for the last iterate and for a (computable) operator norm residual, is $\widetilde{\mathcal{O}}( n + \sqrt{n}L\varepsilon^{-1})$, which improves upon existing methods by a factor up to $\sqrt{n}$. This constitutes the first variance reduction-type result for general finite-sum monotone inclusions and for more specific problems such as convex-concave optimization when operator norm residual is the optimality measure. We further argue that, up to poly-logarithmic factors, this complexity is unimprovable in the monotone Lipschitz setting; i.e., the provided result is near-optimal.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge