Variance-Based Risk Estimations in Markov Processes via Transformation with State Lumping

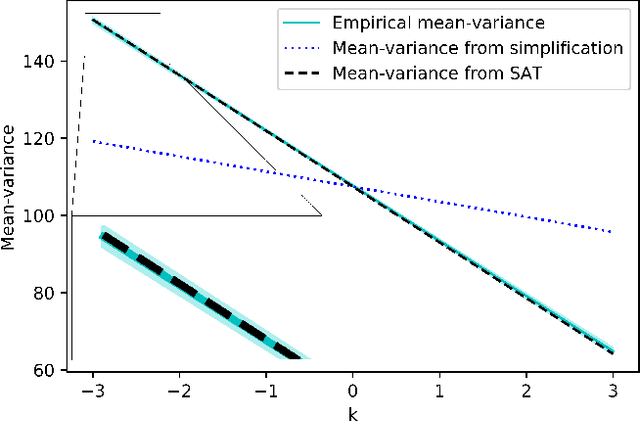
Variance plays a crucial role in risk-sensitive reinforcement learning, and most risk measures can be analyzed via variance. In this paper, we consider two law-invariant risks as examples: mean-variance risk and exponential utility risk. With the aid of the state-augmentation transformation (SAT), we show that, the two risks can be estimated in Markov decision processes (MDPs) with a stochastic transition-based reward and a randomized policy. To relieve the enlarged state space, a novel definition of isotopic states is proposed for state lumping, considering the special structure of the transformed transition probability. In the numerical experiment, we illustrate state lumping in the SAT, errors from a naive reward simplification, and the validity of the SAT for the two risk estimations.