Valid Inference after Causal Discovery
Paper and Code
Aug 11, 2022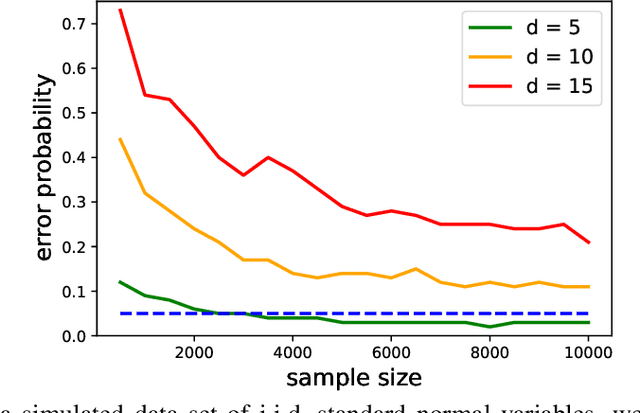

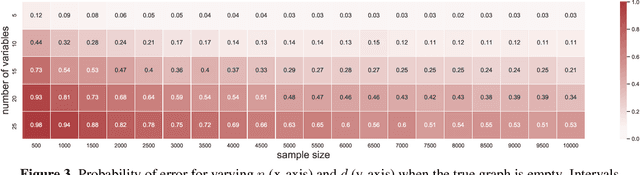
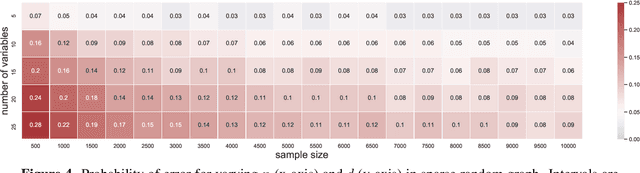
Causal graph discovery and causal effect estimation are two fundamental tasks in causal inference. While many methods have been developed for each task individually, statistical challenges arise when applying these methods jointly: estimating causal effects after running causal discovery algorithms on the same data leads to "double dipping," invalidating coverage guarantees of classical confidence intervals. To this end, we develop tools for valid post-causal-discovery inference. One key contribution is a randomized version of the greedy equivalence search (GES) algorithm, which permits a valid, finite-sample correction of classical confidence intervals. Across empirical studies, we show that a naive combination of causal discovery and subsequent inference algorithms typically leads to highly inflated miscoverage rates; at the same time, our noisy GES method provides reliable coverage control while achieving more accurate causal graph recovery than data splitting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge