Upper Confidence Bounds for Combining Stochastic Bandits
Paper and Code
Dec 24, 2020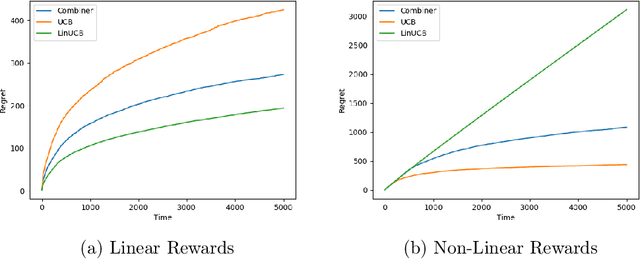
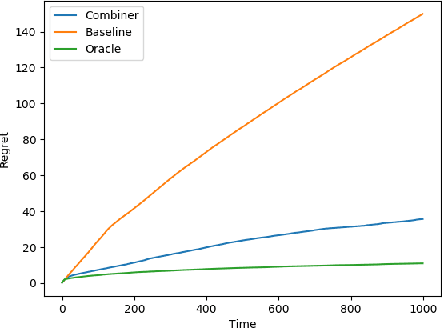
We provide a simple method to combine stochastic bandit algorithms. Our approach is based on a "meta-UCB" procedure that treats each of $N$ individual bandit algorithms as arms in a higher-level $N$-armed bandit problem that we solve with a variant of the classic UCB algorithm. Our final regret depends only on the regret of the base algorithm with the best regret in hindsight. This approach provides an easy and intuitive alternative strategy to the CORRAL algorithm for adversarial bandits, without requiring the stability conditions imposed by CORRAL on the base algorithms. Our results match lower bounds in several settings, and we provide empirical validation of our algorithm on misspecified linear bandit and model selection problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge