Upper Bounding Barlow Twins: A Novel Filter for Multi-Relational Clustering
Paper and Code
Dec 21, 2023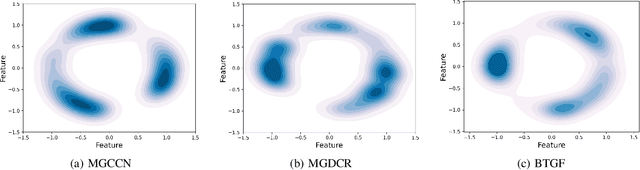
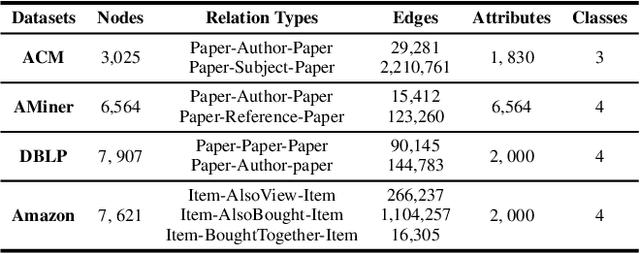
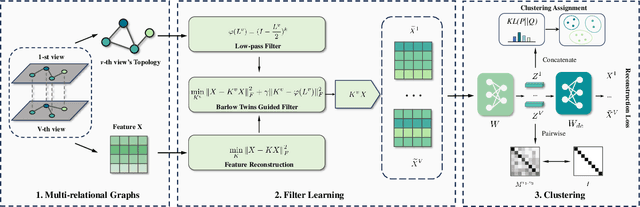
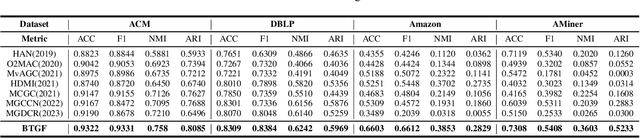
Multi-relational clustering is a challenging task due to the fact that diverse semantic information conveyed in multi-layer graphs is difficult to extract and fuse. Recent methods integrate topology structure and node attribute information through graph filtering. However, they often use a low-pass filter without fully considering the correlation among multiple graphs. To overcome this drawback, we propose to learn a graph filter motivated by the theoretical analysis of Barlow Twins. We find that input with a negative semi-definite inner product provides a lower bound for Barlow Twins loss, which prevents it from reaching a better solution. We thus learn a filter that yields an upper bound for Barlow Twins. Afterward, we design a simple clustering architecture and demonstrate its state-of-the-art performance on four benchmark datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge