Unsupervised Hypergraph Feature Selection via a Novel Point-Weighting Framework and Low-Rank Representation
Paper and Code
Oct 03, 2018
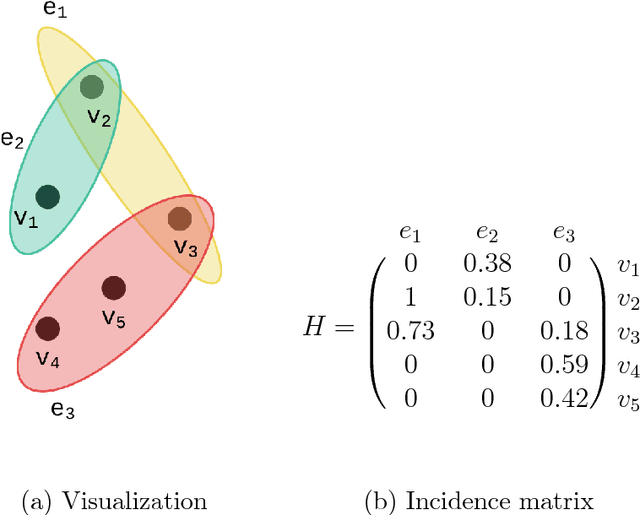
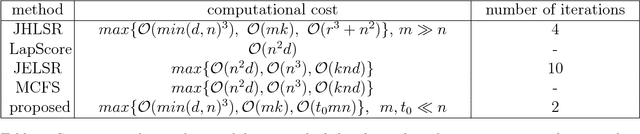
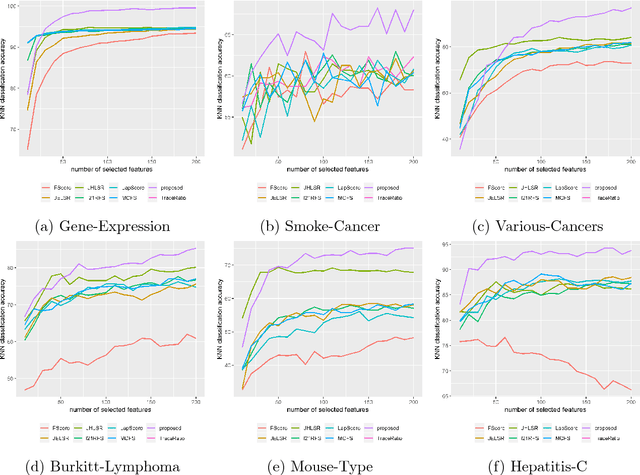
Feature selection methods are widely used in order to solve the 'curse of dimensionality' problem. Many proposed feature selection frameworks, treat all data points equally; neglecting their different representation power and importance. In this paper, we propose an unsupervised hypergraph feature selection method via a novel point-weighting framework and low-rank representation that captures the importance of different data points. We introduce a novel soft hypergraph with low complexity to model data. Then, we formulate the feature selection as an optimization problem to preserve local relationships and also global structure of data. Our approach for global structure preservation helps the framework overcome the problem of unavailability of data labels in unsupervised learning. The proposed feature selection method treats with different data points based on their importance in defining data structure and representation power. Moreover, since the robustness of feature selection methods against noise and outlier is of great importance, we adopt low-rank representation in our model. Also, we provide an efficient algorithm to solve the proposed optimization problem. The computational cost of the proposed algorithm is lower than many state-of-the-art methods which is of high importance in feature selection tasks. We conducted comprehensive experiments with various evaluation methods on different benchmark data sets. These experiments indicate significant improvement, compared with state-of-the-art feature selection methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge