Unsupervised Feature Selection Based on the Morisita Estimator of Intrinsic Dimension
Paper and Code
Jun 02, 2017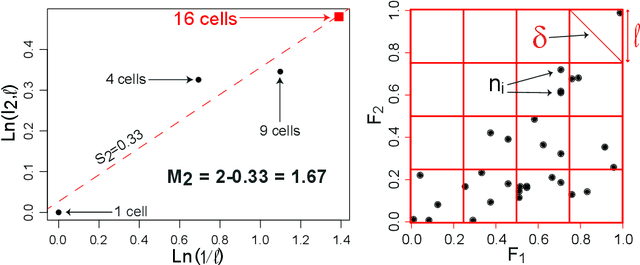

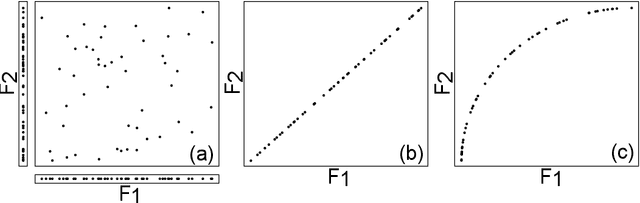
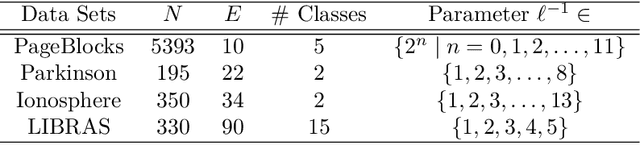
This paper deals with a new filter algorithm for selecting the smallest subset of features carrying all the information content of a data set (i.e. for removing redundant features). It is an advanced version of the fractal dimension reduction technique, and it relies on the recently introduced Morisita estimator of Intrinsic Dimension (ID). Here, the ID is used to quantify dependencies between subsets of features, which allows the effective processing of highly non-linear data. The proposed algorithm is successfully tested on simulated and real world case studies. Different levels of sample size and noise are examined along with the variability of the results. In addition, a comprehensive procedure based on random forests shows that the data dimensionality is significantly reduced by the algorithm without loss of relevant information. And finally, comparisons with benchmark feature selection techniques demonstrate the promising performance of this new filter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge