Unsupervised and Supervised learning by Dense Associative Memory under replica symmetry breaking
Paper and Code
Dec 15, 2023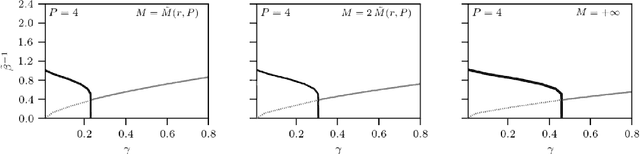

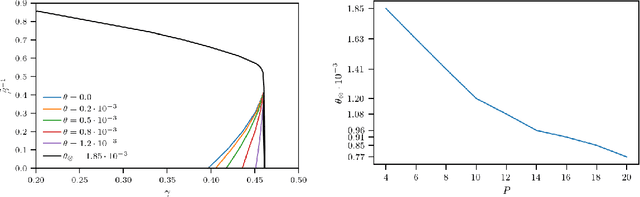

Statistical mechanics of spin glasses is one of the main strands toward a comprehension of information processing by neural networks and learning machines. Tackling this approach, at the fairly standard replica symmetric level of description, recently Hebbian attractor networks with multi-node interactions (often called Dense Associative Memories) have been shown to outperform their classical pairwise counterparts in a number of tasks, from their robustness against adversarial attacks and their capability to work with prohibitively weak signals to their supra-linear storage capacities. Focusing on mathematical techniques more than computational aspects, in this paper we relax the replica symmetric assumption and we derive the one-step broken-replica-symmetry picture of supervised and unsupervised learning protocols for these Dense Associative Memories: a phase diagram in the space of the control parameters is achieved, independently, both via the Parisi's hierarchy within then replica trick as well as via the Guerra's telescope within the broken-replica interpolation. Further, an explicit analytical investigation is provided to deepen both the big-data and ground state limits of these networks as well as a proof that replica symmetry breaking does not alter the thresholds for learning and slightly increases the maximal storage capacity. Finally the De Almeida and Thouless line, depicting the onset of instability of a replica symmetric description, is also analytically derived highlighting how, crossed this boundary, the broken replica description should be preferred.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge