Universal Activation Function For Machine Learning
Paper and Code
Nov 07, 2020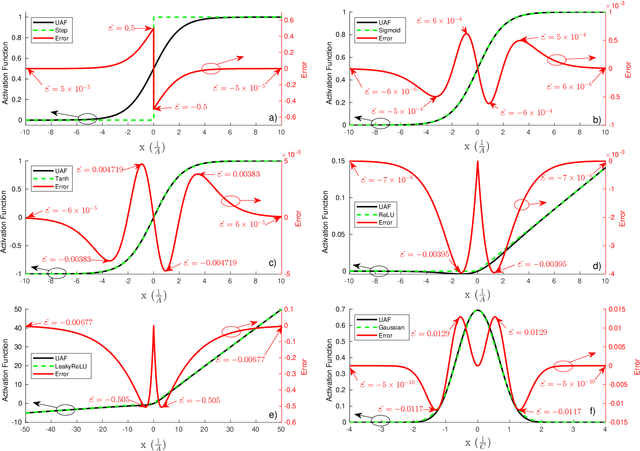
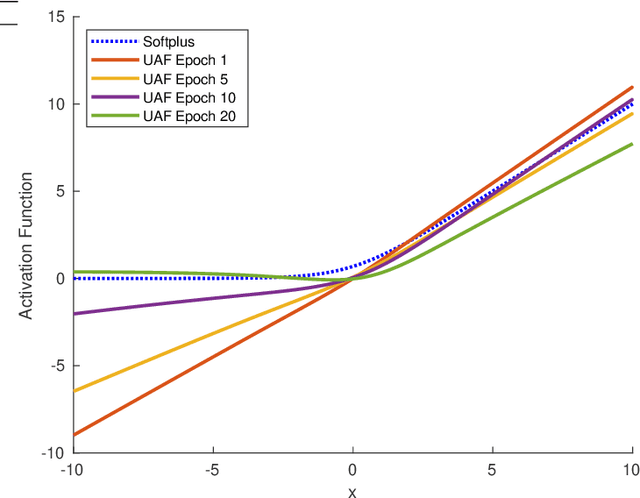
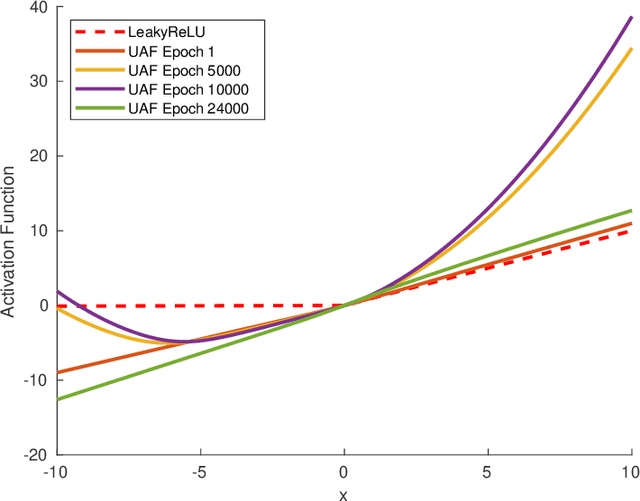
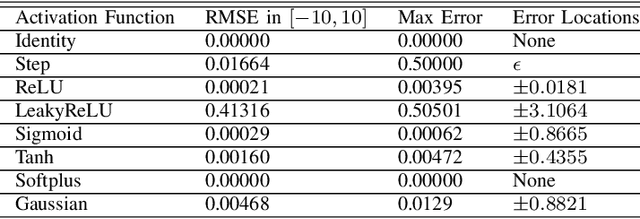
This article proposes a Universal Activation Function (UAF) that achieves near optimal performance in quantification, classification, and reinforcement learning (RL) problems. For any given problem, the optimization algorithms are able to evolve the UAF to a suitable activation function by tuning the UAF's parameters. For the CIFAR-10 classification and VGG-8, the UAF converges to the Mish like activation function, which has near optimal performance $F_{1} = 0.9017\pm0.0040$ when compared to other activation functions. For the quantification of simulated 9-gas mixtures in 30 dB signal-to-noise ratio (SNR) environments, the UAF converges to the identity function, which has near optimal root mean square error of $0.4888 \pm 0.0032$ $\mu M$. In the BipedalWalker-v2 RL dataset, the UAF achieves the 250 reward in $961 \pm 193$ epochs, which proves that the UAF converges in the lowest number of epochs. Furthermore, the UAF converges to a new activation function in the BipedalWalker-v2 RL dataset.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge