Understanding Zipf's law of word frequencies through sample-space collapse in sentence formation
Paper and Code
May 27, 2015

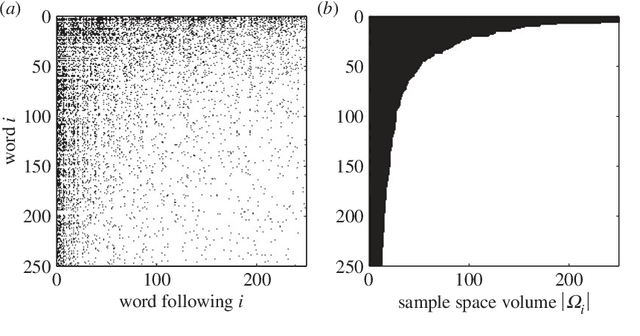
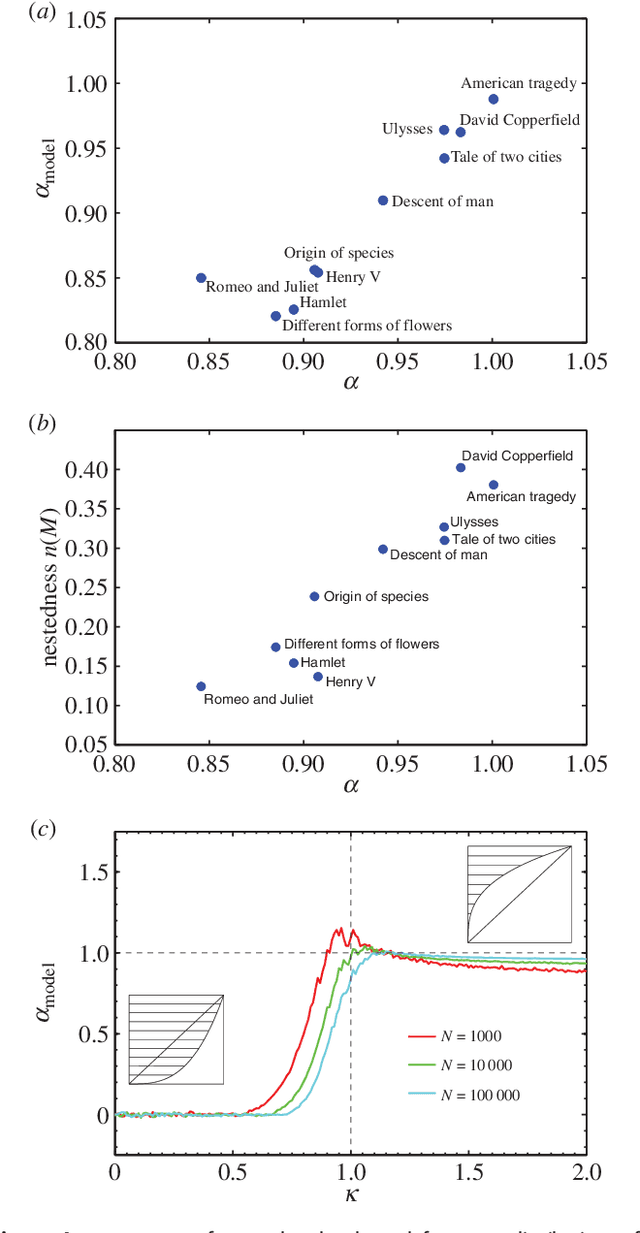
The formation of sentences is a highly structured and history-dependent process. The probability of using a specific word in a sentence strongly depends on the 'history' of word-usage earlier in that sentence. We study a simple history-dependent model of text generation assuming that the sample-space of word usage reduces along sentence formation, on average. We first show that the model explains the approximate Zipf law found in word frequencies as a direct consequence of sample-space reduction. We then empirically quantify the amount of sample-space reduction in the sentences of ten famous English books, by analysis of corresponding word-transition tables that capture which words can follow any given word in a text. We find a highly nested structure in these transition tables and show that this `nestedness' is tightly related to the power law exponents of the observed word frequency distributions. With the proposed model it is possible to understand that the nestedness of a text can be the origin of the actual scaling exponent, and that deviations from the exact Zipf law can be understood by variations of the degree of nestedness on a book-by-book basis. On a theoretical level we are able to show that in case of weak nesting, Zipf's law breaks down in a fast transition. Unlike previous attempts to understand Zipf's law in language the sample-space reducing model is not based on assumptions of multiplicative, preferential, or self-organised critical mechanisms behind language formation, but simply used the empirically quantifiable parameter 'nestedness' to understand the statistics of word frequencies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge