Understanding the Distributions of Aggregation Layers in Deep Neural Networks
Paper and Code
Jul 09, 2021

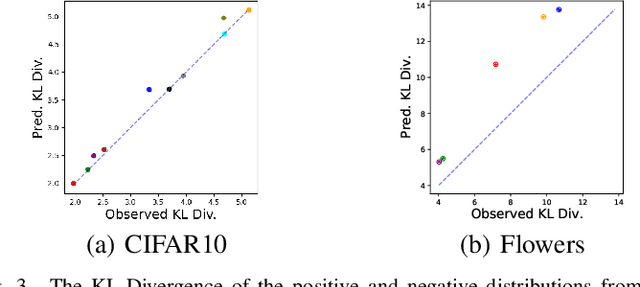
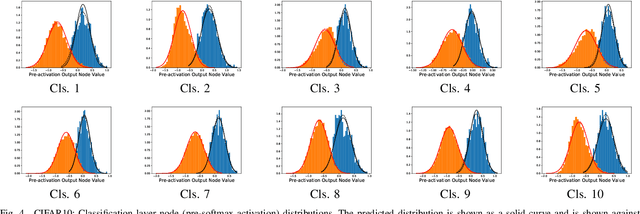
The process of aggregation is ubiquitous in almost all deep nets models. It functions as an important mechanism for consolidating deep features into a more compact representation, whilst increasing robustness to overfitting and providing spatial invariance in deep nets. In particular, the proximity of global aggregation layers to the output layers of DNNs mean that aggregated features have a direct influence on the performance of a deep net. A better understanding of this relationship can be obtained using information theoretic methods. However, this requires the knowledge of the distributions of the activations of aggregation layers. To achieve this, we propose a novel mathematical formulation for analytically modelling the probability distributions of output values of layers involved with deep feature aggregation. An important outcome is our ability to analytically predict the KL-divergence of output nodes in a DNN. We also experimentally verify our theoretical predictions against empirical observations across a range of different classification tasks and datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge