Understanding AdamW through Proximal Methods and Scale-Freeness
Paper and Code
Jan 31, 2022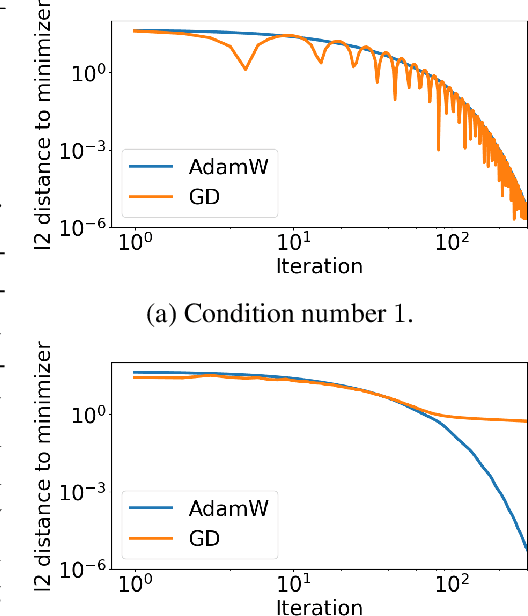

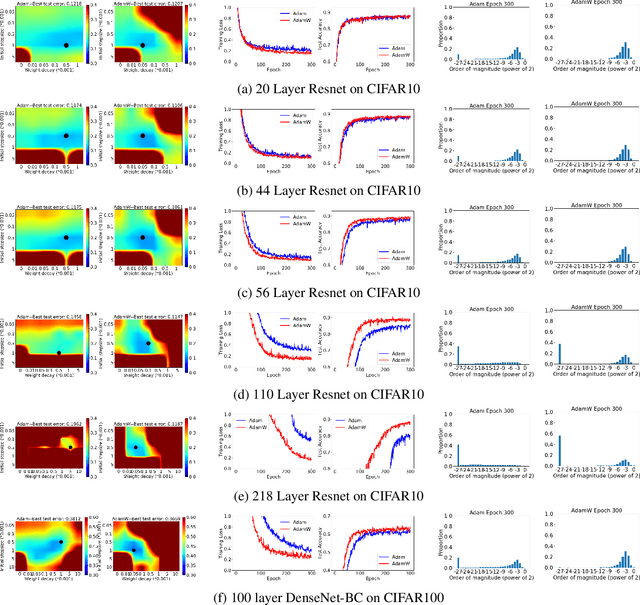
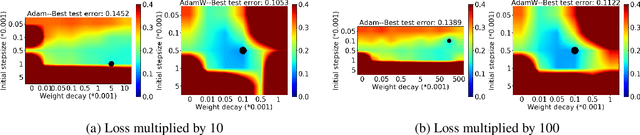
Adam has been widely adopted for training deep neural networks due to less hyperparameter tuning and remarkable performance. To improve generalization, Adam is typically used in tandem with a squared $\ell_2$ regularizer (referred to as Adam-$\ell_2$). However, even better performance can be obtained with AdamW, which decouples the gradient of the regularizer from the update rule of Adam-$\ell_2$. Yet, we are still lacking a complete explanation of the advantages of AdamW. In this paper, we tackle this question from both an optimization and an empirical point of view. First, we show how to re-interpret AdamW as an approximation of a proximal gradient method, which takes advantage of the closed-form proximal mapping of the regularizer instead of only utilizing its gradient information as in Adam-$\ell_2$. Next, we consider the property of "scale-freeness" enjoyed by AdamW and by its proximal counterpart: their updates are invariant to component-wise rescaling of the gradients. We provide empirical evidence across a wide range of deep learning experiments showing a correlation between the problems in which AdamW exhibits an advantage over Adam-$\ell_2$ and the degree to which we expect the gradients of the network to exhibit multiple scales, thus motivating the hypothesis that the advantage of AdamW could be due to the scale-free updates.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge