Undersampling is a Minimax Optimal Robustness Intervention in Nonparametric Classification
Paper and Code
May 26, 2022
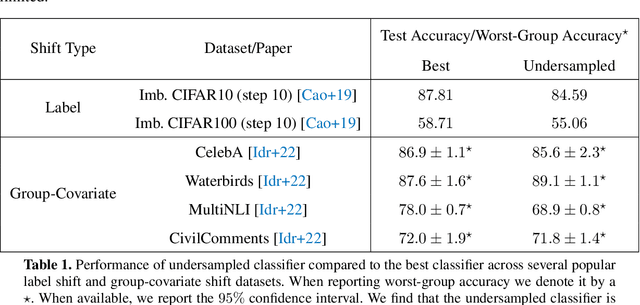
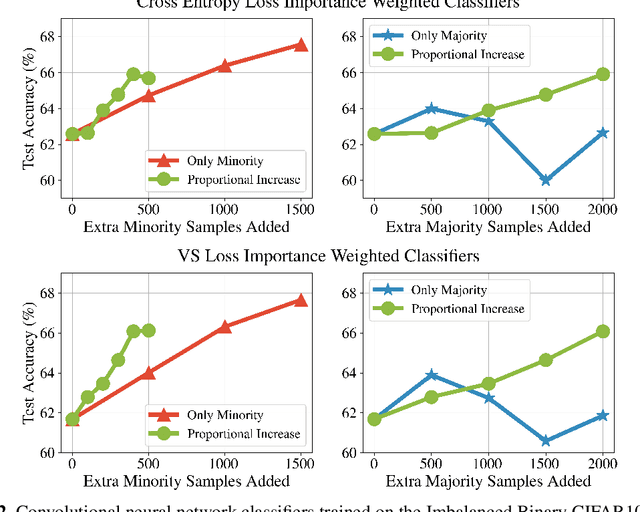

While a broad range of techniques have been proposed to tackle distribution shift, the simple baseline of training on an $\textit{undersampled}$ dataset often achieves close to state-of-the-art-accuracy across several popular benchmarks. This is rather surprising, since undersampling algorithms discard excess majority group data. To understand this phenomenon, we ask if learning is fundamentally constrained by a lack of minority group samples. We prove that this is indeed the case in the setting of nonparametric binary classification. Our results show that in the worst case, an algorithm cannot outperform undersampling unless there is a high degree of overlap between the train and test distributions (which is unlikely to be the case in real-world datasets), or if the algorithm leverages additional structure about the distribution shift. In particular, in the case of label shift we show that there is always an undersampling algorithm that is minimax optimal. While in the case of group-covariate shift we show that there is an undersampling algorithm that is minimax optimal when the overlap between the group distributions is small. We also perform an experimental case study on a label shift dataset and find that in line with our theory the test accuracy of robust neural network classifiers is constrained by the number of minority samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge