Uncertainty in Minimum Cost Multicuts for Image and Motion Segmentation
Paper and Code
May 16, 2021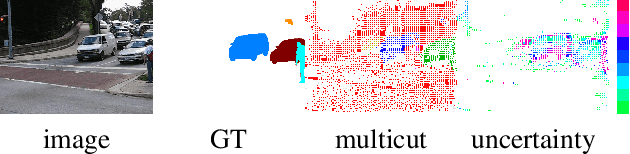


The minimum cost lifted multicut approach has proven practically good performance in a wide range of applications such as image decomposition, mesh segmentation, multiple object tracking, and motion segmentation. It addresses such problems in a graph-based model, where real-valued costs are assigned to the edges between entities such that the minimum cut decomposes the graph into an optimal number of segments. Driven by a probabilistic formulation of minimum cost multicuts, we provide a measure for the uncertainties of the decisions made during the optimization. We argue that access to such uncertainties is crucial for many practical applications and conduct an evaluation by means of sparsifications on three different, widely used datasets in the context of image decomposition (BSDS-500) and motion segmentation (DAVIS2016 and FBMS59) in terms of variation of information (VI) and Rand index (RI).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge