Unbiased Learning of Deep Generative Models with Structured Discrete Representations

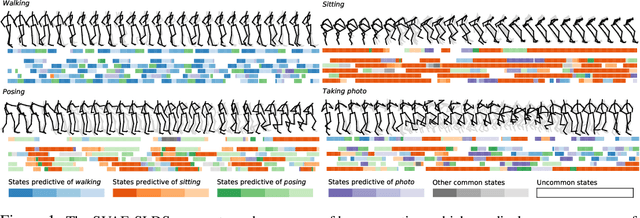
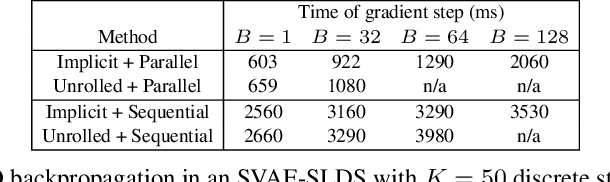
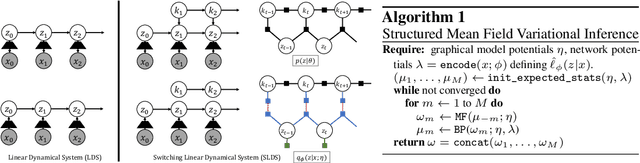
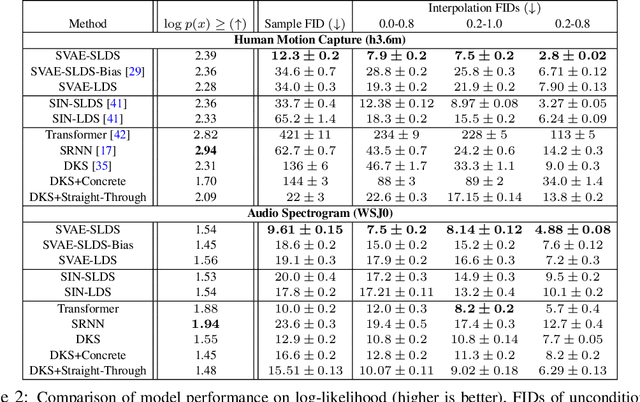
By composing graphical models with deep learning architectures, we learn generative models with the strengths of both frameworks. The structured variational autoencoder (SVAE) inherits structure and interpretability from graphical models, and flexible likelihoods for high-dimensional data from deep learning, but poses substantial optimization challenges. We propose novel algorithms for learning SVAEs, and are the first to demonstrate the SVAE's ability to handle multimodal uncertainty when data is missing by incorporating discrete latent variables. Our memory-efficient implicit differentiation scheme makes the SVAE tractable to learn via gradient descent, while demonstrating robustness to incomplete optimization. To more rapidly learn accurate graphical model parameters, we derive a method for computing natural gradients without manual derivations, which avoids biases found in prior work. These optimization innovations enable the first comparisons of the SVAE to state-of-the-art time series models, where the SVAE performs competitively while learning interpretable and structured discrete data representations.