TzK: Flow-Based Conditional Generative Model
Paper and Code
Mar 14, 2019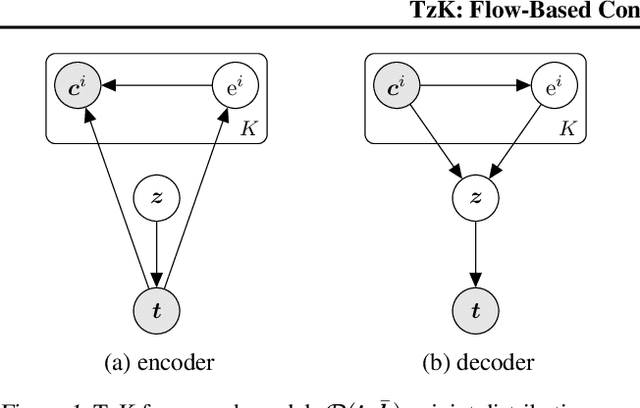
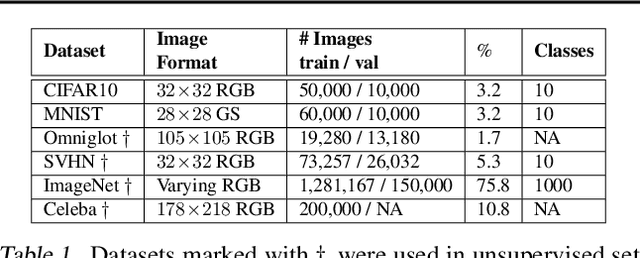


We formulate a new class of conditional generative models based on probability flows. Trained with maximum likelihood, it provides efficient inference and sampling from class-conditionals or the joint distribution, and does not require a priori knowledge of the number of classes or the relationships between classes. This allows one to train generative models from multiple, heterogeneous datasets, while retaining strong prior models over subsets of the data (e.g., from a single dataset, class label, or attribute). In this paper, in addition to end-to-end learning, we show how one can learn a single model from multiple datasets with a relatively weak Glow architecture, and then extend it by conditioning on different knowledge types (e.g., a single dataset). This yields log likelihood comparable to state-of-the-art, compelling samples from conditional priors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge