Twenty (simple) questions
Paper and Code
Apr 25, 2017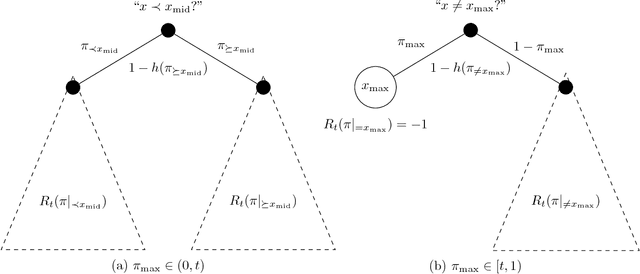
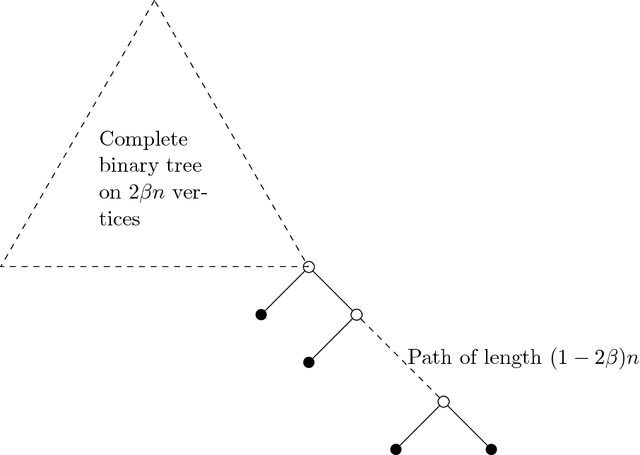
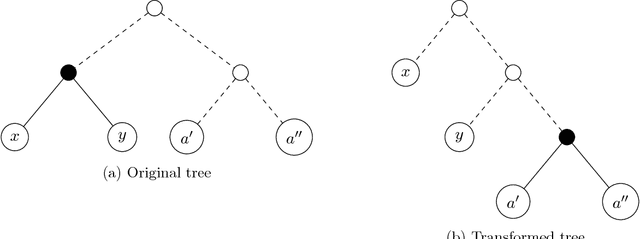
A basic combinatorial interpretation of Shannon's entropy function is via the "20 questions" game. This cooperative game is played by two players, Alice and Bob: Alice picks a distribution $\pi$ over the numbers $\{1,\ldots,n\}$, and announces it to Bob. She then chooses a number $x$ according to $\pi$, and Bob attempts to identify $x$ using as few Yes/No queries as possible, on average. An optimal strategy for the "20 questions" game is given by a Huffman code for $\pi$: Bob's questions reveal the codeword for $x$ bit by bit. This strategy finds $x$ using fewer than $H(\pi)+1$ questions on average. However, the questions asked by Bob could be arbitrary. In this paper, we investigate the following question: Are there restricted sets of questions that match the performance of Huffman codes, either exactly or approximately? Our first main result shows that for every distribution $\pi$, Bob has a strategy that uses only questions of the form "$x < c$?" and "$x = c$?", and uncovers $x$ using at most $H(\pi)+1$ questions on average, matching the performance of Huffman codes in this sense. We also give a natural set of $O(rn^{1/r})$ questions that achieve a performance of at most $H(\pi)+r$, and show that $\Omega(rn^{1/r})$ questions are required to achieve such a guarantee. Our second main result gives a set $\mathcal{Q}$ of $1.25^{n+o(n)}$ questions such that for every distribution $\pi$, Bob can implement an optimal strategy for $\pi$ using only questions from $\mathcal{Q}$. We also show that $1.25^{n-o(n)}$ questions are needed, for infinitely many $n$. If we allow a small slack of $r$ over the optimal strategy, then roughly $(rn)^{\Theta(1/r)}$ questions are necessary and sufficient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge