Transformed Residual Quantization for Approximate Nearest Neighbor Search
Paper and Code
Dec 22, 2015

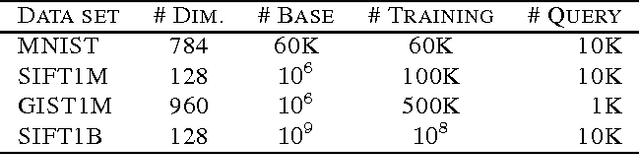

The success of product quantization (PQ) for fast nearest neighbor search depends on the exponentially reduced complexities of both storage and computation with respect to the codebook size. Recent efforts have been focused on employing sophisticated optimization strategies, or seeking more effective models. Residual quantization (RQ) is such an alternative that holds the same property as PQ in terms of the aforementioned complexities. In addition to being a direct replacement of PQ, hybrids of PQ and RQ can yield more gains for approximate nearest neighbor search. This motivated us to propose a novel approach to optimizing RQ and the related hybrid models. With an observation of the general randomness increase in a residual space, we propose a new strategy that jointly learns a local transformation per residual cluster with an ultimate goal to reduce overall quantization errors. We have shown that our approach can achieve significantly better accuracy on nearest neighbor search than both the original and the optimized PQ on several very large scale benchmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge