Transfer learning with high-dimensional quantile regression
Paper and Code
Nov 26, 2022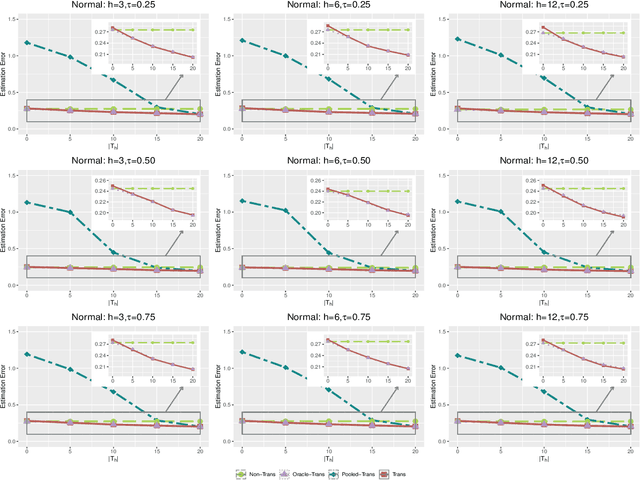
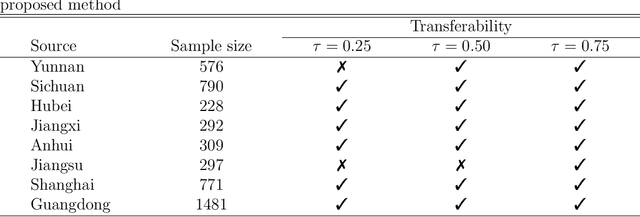
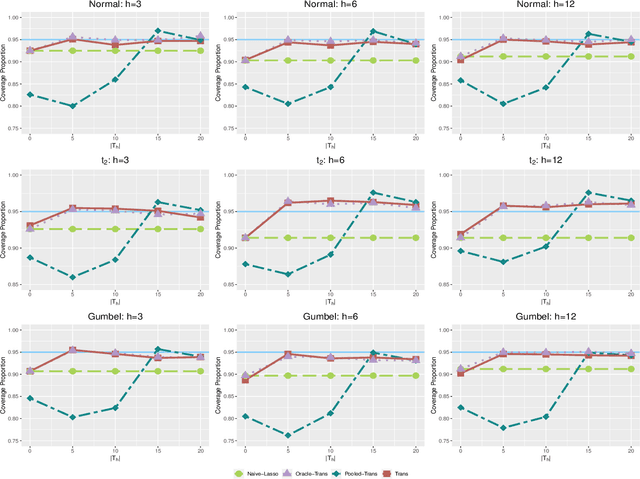
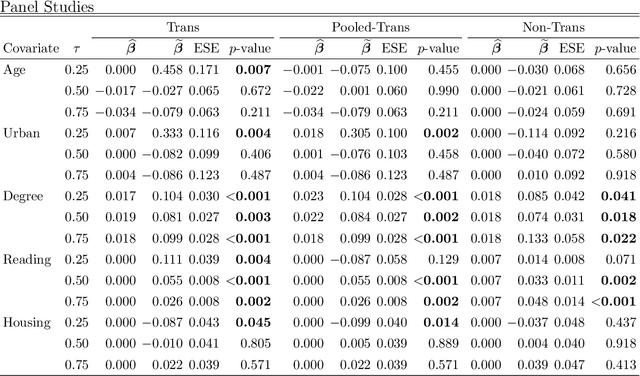
Transfer learning has become an essential technique to exploit information from the source domain to boost performance of the target task. Despite the prevalence in high-dimensional data, heterogeneity and/or heavy tails tend to be discounted in current transfer learning approaches and thus may undermine the resulting performance. We propose a transfer learning procedure in the framework of high-dimensional quantile regression models to accommodate the heterogeneity and heavy tails in the source and target domains. We establish error bounds of the transfer learning estimator based on delicately selected transferable source domains, showing that lower error bounds can be achieved for critical selection criterion and larger sample size of source tasks. We further propose valid confidence interval and hypothesis test procedures for individual component of quantile regression coefficients by advocating a one-step debiased estimator of transfer learning estimator wherein the consistent variance estimation is proposed via the technique of transfer learning again. Simulation results demonstrate that the proposed method exhibits some favorable performances.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge