Transfer Learning in Information Criteria-based Feature Selection
Paper and Code
Jul 06, 2021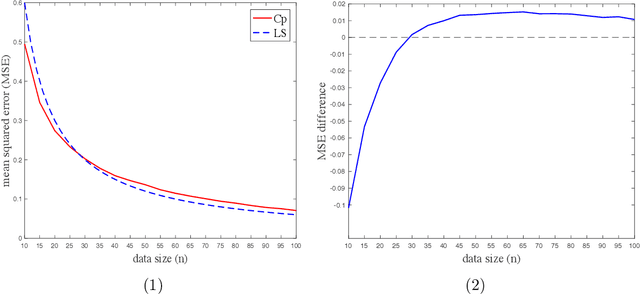
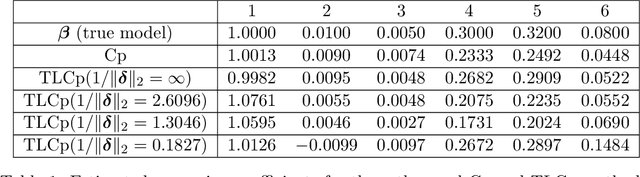
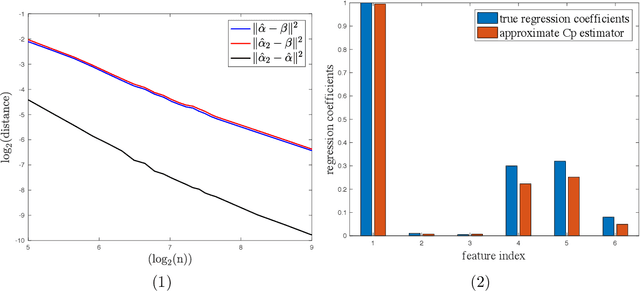
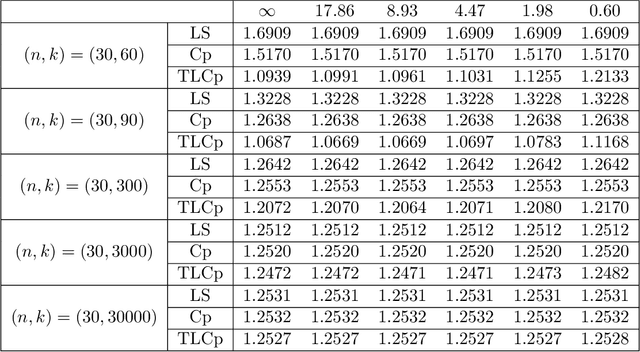
This paper investigates the effectiveness of transfer learning based on Mallows' Cp. We propose a procedure that combines transfer learning with Mallows' Cp (TLCp) and prove that it outperforms the conventional Mallows' Cp criterion in terms of accuracy and stability. Our theoretical results indicate that, for any sample size in the target domain, the proposed TLCp estimator performs better than the Cp estimator by the mean squared error (MSE) metric in the case of orthogonal predictors, provided that i) the dissimilarity between the tasks from source domain and target domain is small, and ii) the procedure parameters (complexity penalties) are tuned according to certain explicit rules. Moreover, we show that our transfer learning framework can be extended to other feature selection criteria, such as the Bayesian information criterion. By analyzing the solution of the orthogonalized Cp, we identify an estimator that asymptotically approximates the solution of the Cp criterion in the case of non-orthogonal predictors. Similar results are obtained for the non-orthogonal TLCp. Finally, simulation studies and applications with real data demonstrate the usefulness of the TLCp scheme.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge