Transfer Learning for Linear Regression: a Statistical Test of Gain
Paper and Code
Feb 18, 2021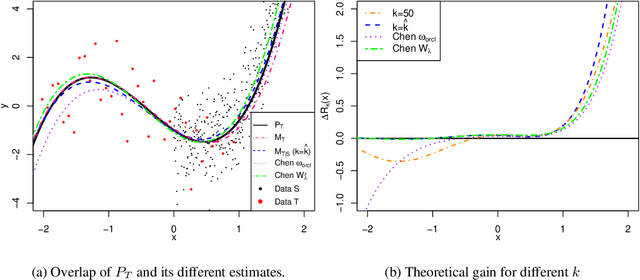
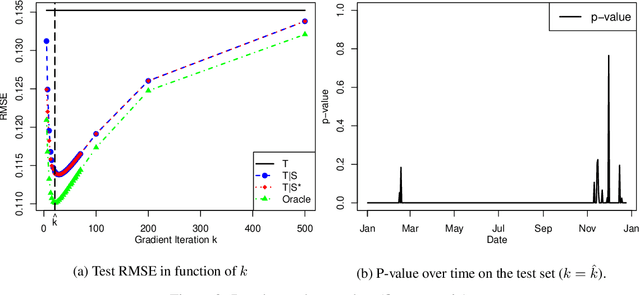
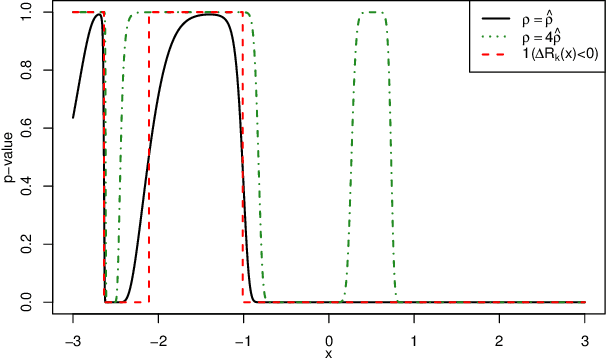
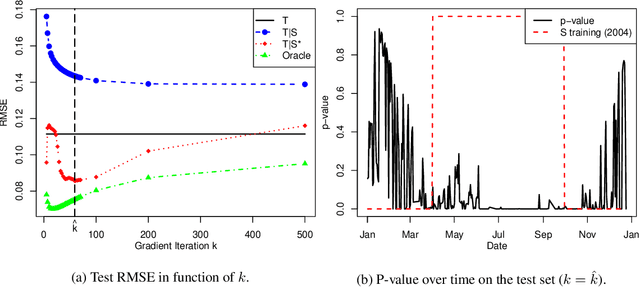
Transfer learning, also referred as knowledge transfer, aims at reusing knowledge from a source dataset to a similar target one. While many empirical studies illustrate the benefits of transfer learning, few theoretical results are established especially for regression problems. In this paper a theoretical framework for the problem of parameter transfer for the linear model is proposed. It is shown that the quality of transfer for a new input vector $x$ depends on its representation in an eigenbasis involving the parameters of the problem. Furthermore a statistical test is constructed to predict whether a fine-tuned model has a lower prediction quadratic risk than the base target model for an unobserved sample. Efficiency of the test is illustrated on synthetic data as well as real electricity consumption data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge