Transfer Learning for High-dimensional Linear Regression: Prediction, Estimation, and Minimax Optimality
Paper and Code
Jun 18, 2020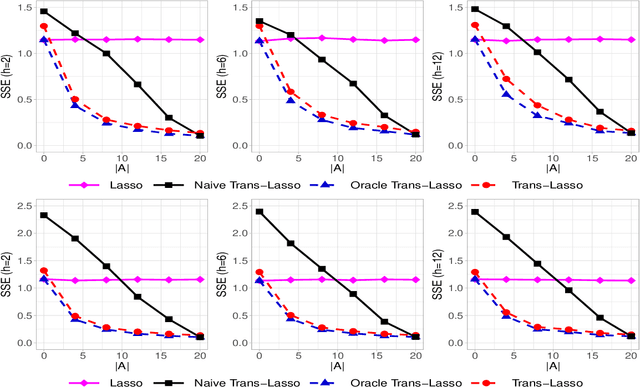
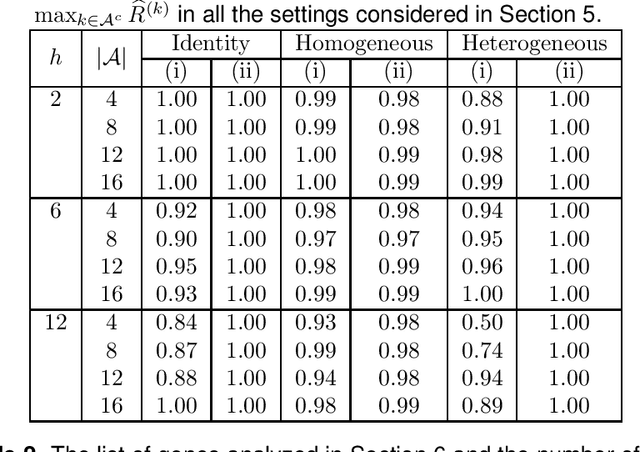
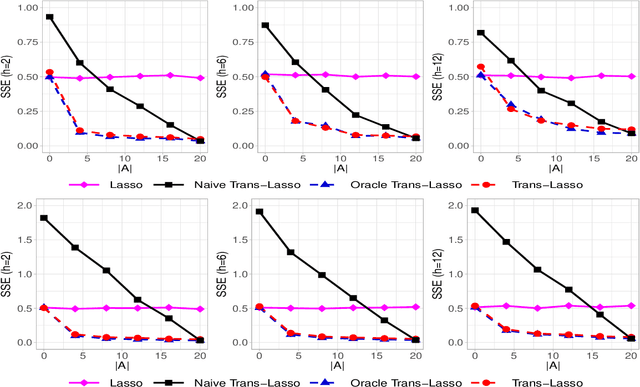
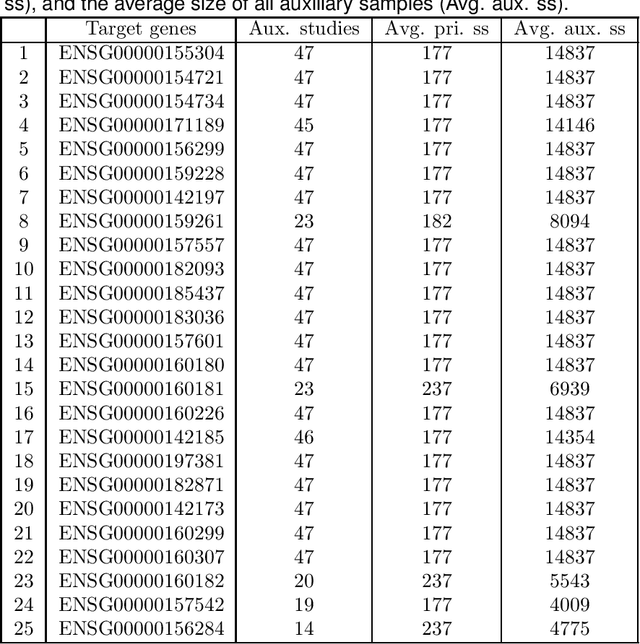
This paper considers the estimation and prediction of a high-dimensional linear regression in the setting of transfer learning, using samples from the target model as well as auxiliary samples from different but possibly related regression models. When the set of "informative" auxiliary samples is known, an estimator and a predictor are proposed and their optimality is established. The optimal rates of convergence for prediction and estimation are faster than the corresponding rates without using the auxiliary samples. This implies that knowledge from the informative auxiliary samples can be transferred to improve the learning performance of the target problem. In the case that the set of informative auxiliary samples is unknown, we propose a data-driven procedure for transfer learning, called Trans-Lasso, and reveal its robustness to non-informative auxiliary samples and its efficiency in knowledge transfer. The proposed procedures are demonstrated in numerical studies and are applied to a dataset concerning the associations among gene expressions. It is shown that Trans-Lasso leads to improved performance in gene expression prediction in a target tissue by incorporating the data from multiple different tissues as auxiliary samples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge