Trajectory Synthesis for Fisher Information Maximization
Paper and Code
Sep 11, 2017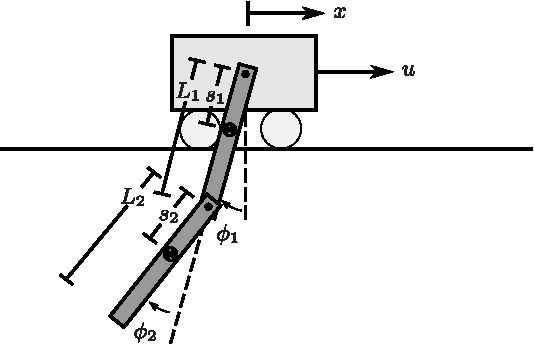



Estimation of model parameters in a dynamic system can be significantly improved with the choice of experimental trajectory. For general, nonlinear dynamic systems, finding globally "best" trajectories is typically not feasible; however, given an initial estimate of the model parameters and an initial trajectory, we present a continuous-time optimization method that produces a locally optimal trajectory for parameter estimation in the presence of measurement noise. The optimization algorithm is formulated to find system trajectories that improve a norm on the Fisher information matrix. A double-pendulum cart apparatus is used to numerically and experimentally validate this technique. In simulation, the optimized trajectory increases the minimum eigenvalue of the Fisher information matrix by three orders of magnitude compared to the initial trajectory. Experimental results show that this optimized trajectory translates to an order of magnitude improvement in the parameter estimate error in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge