Training OOD Detectors in their Natural Habitats

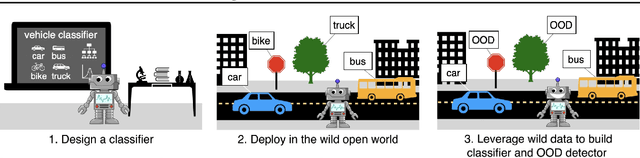
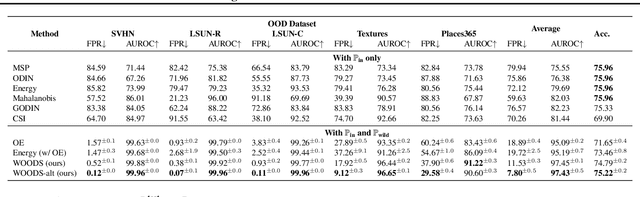
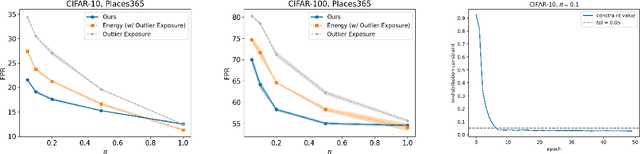
Out-of-distribution (OOD) detection is important for machine learning models deployed in the wild. Recent methods use auxiliary outlier data to regularize the model for improved OOD detection. However, these approaches make a strong distributional assumption that the auxiliary outlier data is completely separable from the in-distribution (ID) data. In this paper, we propose a novel framework that leverages wild mixture data -- that naturally consists of both ID and OOD samples. Such wild data is abundant and arises freely upon deploying a machine learning classifier in their \emph{natural habitats}. Our key idea is to formulate a constrained optimization problem and to show how to tractably solve it. Our learning objective maximizes the OOD detection rate, subject to constraints on the classification error of ID data and on the OOD error rate of ID examples. We extensively evaluate our approach on common OOD detection tasks and demonstrate superior performance.