Training Neural Networks Without Gradients: A Scalable ADMM Approach
Paper and Code
May 06, 2016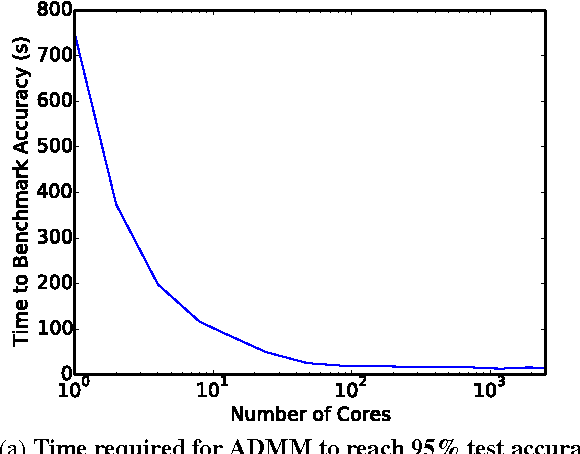
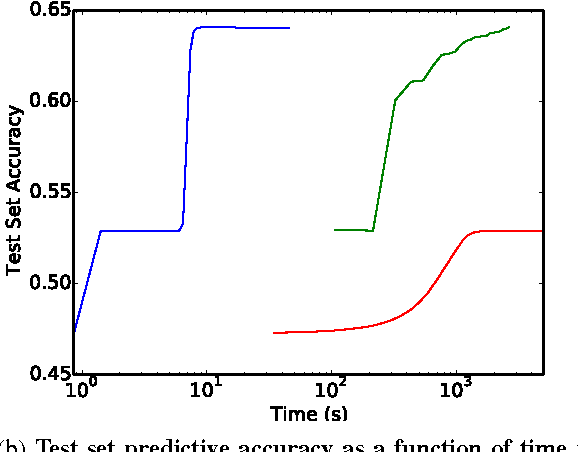
With the growing importance of large network models and enormous training datasets, GPUs have become increasingly necessary to train neural networks. This is largely because conventional optimization algorithms rely on stochastic gradient methods that don't scale well to large numbers of cores in a cluster setting. Furthermore, the convergence of all gradient methods, including batch methods, suffers from common problems like saturation effects, poor conditioning, and saddle points. This paper explores an unconventional training method that uses alternating direction methods and Bregman iteration to train networks without gradient descent steps. The proposed method reduces the network training problem to a sequence of minimization sub-steps that can each be solved globally in closed form. The proposed method is advantageous because it avoids many of the caveats that make gradient methods slow on highly non-convex problems. The method exhibits strong scaling in the distributed setting, yielding linear speedups even when split over thousands of cores.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge