Training for the Future: A Simple Gradient Interpolation Loss to Generalize Along Time
Paper and Code
Aug 15, 2021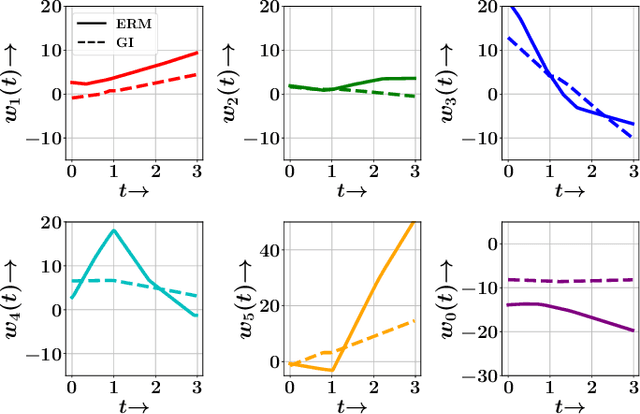
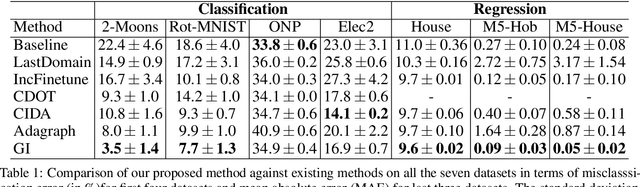
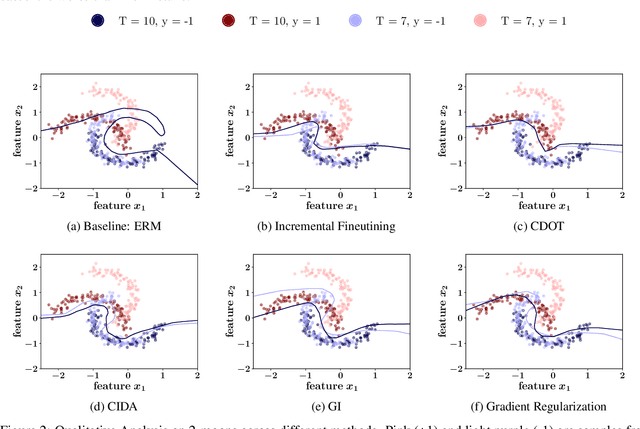
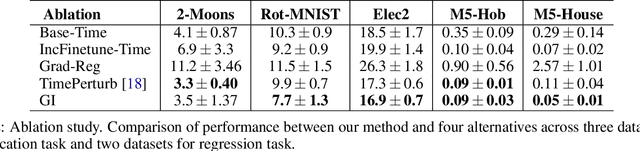
In several real world applications, machine learning models are deployed to make predictions on data whose distribution changes gradually along time, leading to a drift between the train and test distributions. Such models are often re-trained on new data periodically, and they hence need to generalize to data not too far into the future. In this context, there is much prior work on enhancing temporal generalization, e.g. continuous transportation of past data, kernel smoothed time-sensitive parameters and more recently, adversarial learning of time-invariant features. However, these methods share several limitations, e.g, poor scalability, training instability, and dependence on unlabeled data from the future. Responding to the above limitations, we propose a simple method that starts with a model with time-sensitive parameters but regularizes its temporal complexity using a Gradient Interpolation (GI) loss. GI allows the decision boundary to change along time and can still prevent overfitting to the limited training time snapshots by allowing task-specific control over changes along time. We compare our method to existing baselines on multiple real-world datasets, which show that GI outperforms more complicated generative and adversarial approaches on the one hand, and simpler gradient regularization methods on the other.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge