Trading Positional Complexity vs. Deepness in Coordinate Networks
Paper and Code
May 18, 2022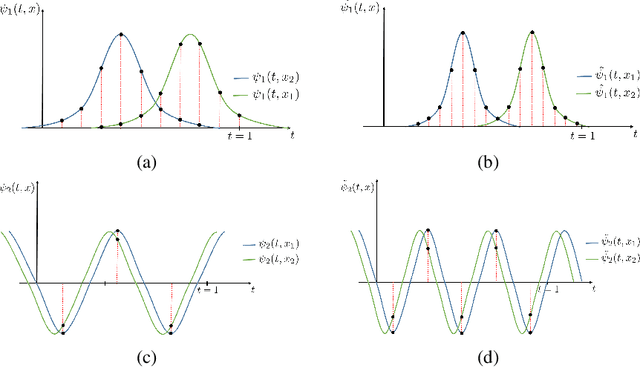
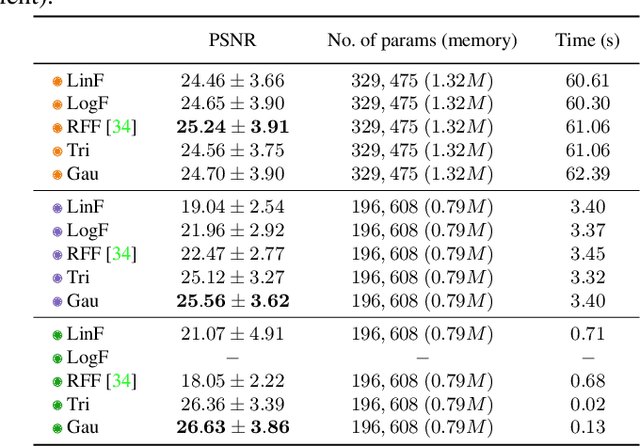
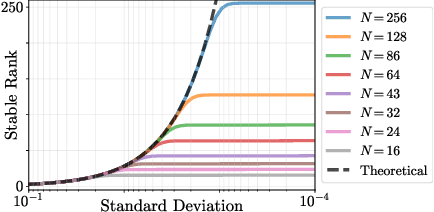
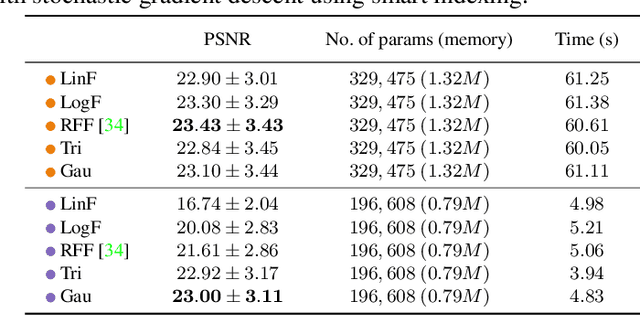
It is well noted that coordinate-based MLPs benefit -- in terms of preserving high-frequency information -- through the encoding of coordinate positions as an array of Fourier features. Hitherto, the rationale for the effectiveness of these positional encodings has been mainly studied through a Fourier lens. In this paper, we strive to broaden this understanding by showing that alternative non-Fourier embedding functions can indeed be used for positional encoding. Moreover, we show that their performance is entirely determined by a trade-off between the stable rank of the embedded matrix and the distance preservation between embedded coordinates. We further establish that the now ubiquitous Fourier feature mapping of position is a special case that fulfills these conditions. Consequently, we present a more general theory to analyze positional encoding in terms of shifted basis functions. In addition, we argue that employing a more complex positional encoding -- that scales exponentially with the number of modes -- requires only a linear (rather than deep) coordinate function to achieve comparable performance. Counter-intuitively, we demonstrate that trading positional embedding complexity for network deepness is orders of magnitude faster than current state-of-the-art; despite the additional embedding complexity. To this end, we develop the necessary theoretical formulae and empirically verify that our theoretical claims hold in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge