Towards Understanding the Spectral Bias of Deep Learning

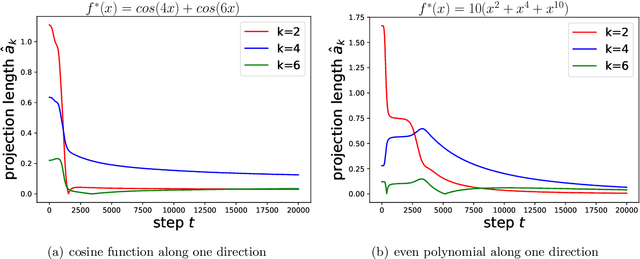
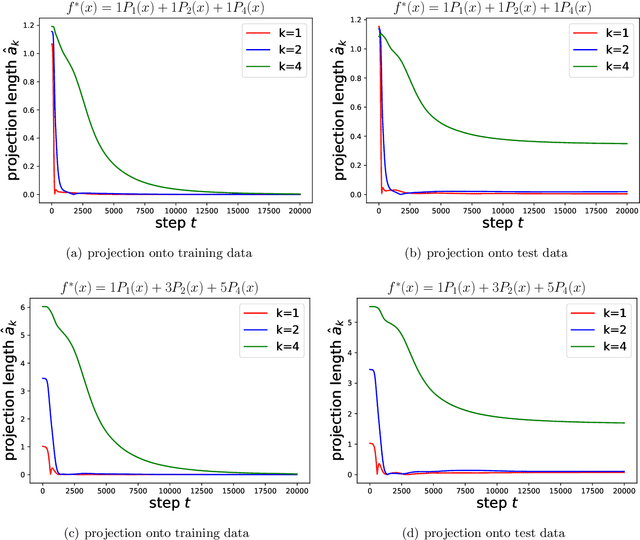
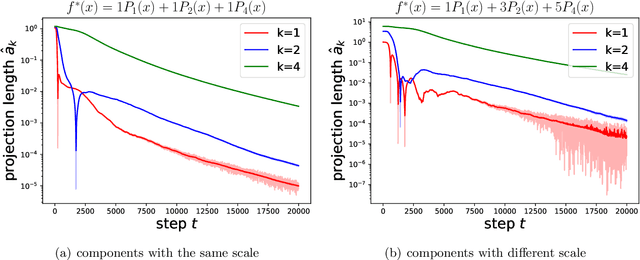
An intriguing phenomenon observed during training neural networks is the spectral bias, where neural networks are biased towards learning less complex functions. The priority of learning functions with low complexity might be at the core of explaining generalization ability of neural network, and certain efforts have been made to provide theoretical explanation for spectral bias. However, there is still no satisfying theoretical result justifying the underlying mechanism of spectral bias. In this paper, we give a comprehensive and rigorous explanation for spectral bias and relate it with the neural tangent kernel function proposed in recent work. We prove that the training process of neural networks can be decomposed along different directions defined by the eigenfunctions of the neural tangent kernel, where each direction has its own convergence rate and the rate is determined by the corresponding eigenvalue. We then provide a case study when the input data is uniformly distributed over the unit sphere, and show that lower degree spherical harmonics are easier to be learned by over-parameterized neural networks.