Towards Understanding Linear Value Decomposition in Cooperative Multi-Agent Q-Learning

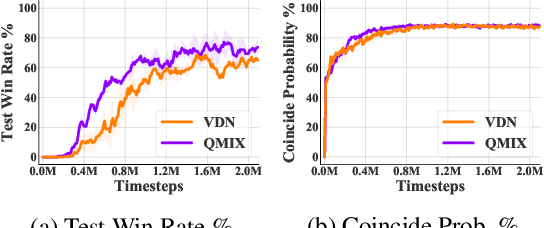
Value decomposition is a popular and promising approach to scaling up multi-agent reinforcement learning in cooperative settings. However, the theoretical understanding of such methods is limited. In this paper, we introduce a variant of the fitted Q-iteration framework for analyzing multi-agent Q-learning with value decomposition. Based on this framework, we derive a closed-form solution to the Bellman error minimization with linear value decomposition. With this novel solution, we further reveal two interesting insights: 1) linear value decomposition implicitly implements a classical multi-agent credit assignment called counterfactual difference rewards; and 2) multi-agent Q-learning with linear value decomposition requires on-policy data distribution to achieve numerical stability. In the empirical study, our experiments demonstrate the realizability of our theoretical implications in a broad set of complicated tasks. They show that most state-of-the-art deep multi-agent Q-learning algorithms using linear value decomposition cannot efficiently utilize off-policy samples, which may even lead to an unbounded divergence.