Towards NNGP-guided Neural Architecture Search
Paper and Code
Nov 11, 2020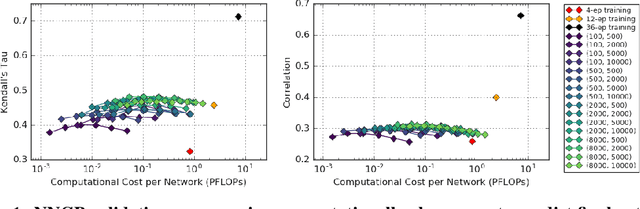
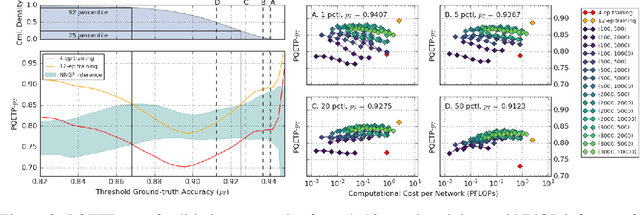
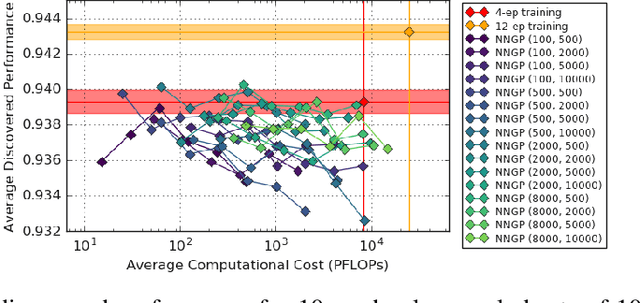

The predictions of wide Bayesian neural networks are described by a Gaussian process, known as the Neural Network Gaussian Process (NNGP). Analytic forms for NNGP kernels are known for many models, but computing the exact kernel for convolutional architectures is prohibitively expensive. One can obtain effective approximations of these kernels through Monte-Carlo estimation using finite networks at initialization. Monte-Carlo NNGP inference is orders-of-magnitude cheaper in FLOPs compared to gradient descent training when the dataset size is small. Since NNGP inference provides a cheap measure of performance of a network architecture, we investigate its potential as a signal for neural architecture search (NAS). We compute the NNGP performance of approximately 423k networks in the NAS-bench 101 dataset on CIFAR-10 and compare its utility against conventional performance measures obtained by shortened gradient-based training. We carry out a similar analysis on 10k randomly sampled networks in the mobile neural architecture search (MNAS) space for ImageNet. We discover comparative advantages of NNGP-based metrics, and discuss potential applications. In particular, we propose that NNGP performance is an inexpensive signal independent of metrics obtained from training that can either be used for reducing big search spaces, or improving training-based performance measures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge