Towards Learning Controllable Representations of Physical Systems
Paper and Code
Nov 24, 2020


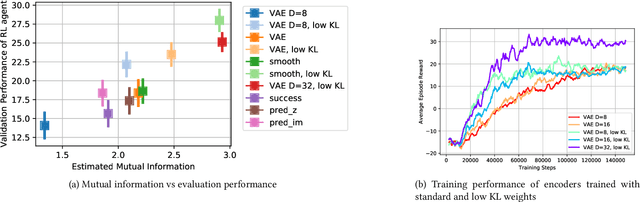
Learned representations of dynamical systems reduce dimensionality, potentially supporting downstream reinforcement learning (RL). However, no established methods predict a representation's suitability for control and evaluation is largely done via downstream RL performance, slowing representation design. Towards a principled evaluation of representations for control, we consider the relationship between the true state and the corresponding representations, proposing that ideally each representation corresponds to a unique true state. This motivates two metrics: temporal smoothness and high mutual information between true state/representation. These metrics are related to established representation objectives, and studied on Lagrangian systems where true state, information requirements, and statistical properties of the state can be formalized for a broad class of systems. These metrics are shown to predict reinforcement learning performance in a simulated peg-in-hole task when comparing variants of autoencoder-based representations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge