Towards Generalized Inverse Reinforcement Learning
Paper and Code
Feb 11, 2024

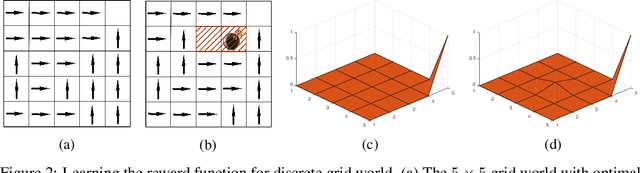

This paper studies generalized inverse reinforcement learning (GIRL) in Markov decision processes (MDPs), that is, the problem of learning the basic components of an MDP given observed behavior (policy) that might not be optimal. These components include not only the reward function and transition probability matrices, but also the action space and state space that are not exactly known but are known to belong to given uncertainty sets. We address two key challenges in GIRL: first, the need to quantify the discrepancy between the observed policy and the underlying optimal policy; second, the difficulty of mathematically characterizing the underlying optimal policy when the basic components of an MDP are unobservable or partially observable. Then, we propose the mathematical formulation for GIRL and develop a fast heuristic algorithm. Numerical results on both finite and infinite state problems show the merit of our formulation and algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge