Towards GANs' Approximation Ability

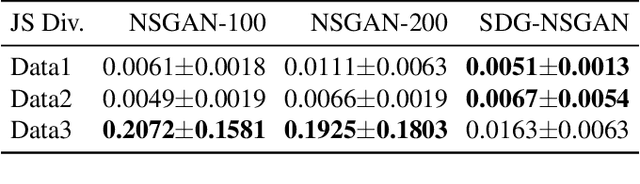
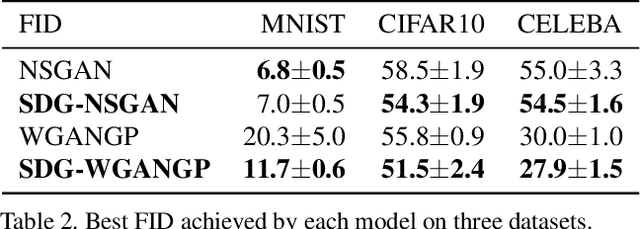
Generative adversarial networks (GANs) have attracted intense interest in the field of generative models. However, few investigations focusing either on the theoretical analysis or on algorithm design for the approximation ability of the generator of GANs have been reported. This paper will first theoretically analyze GANs' approximation property. Similar to the universal approximation property of the full connected neural networks with one hidden layer, we prove that the generator with the input latent variable in GANs can universally approximate the potential data distribution given the increasing hidden neurons. Furthermore, we propose an approach named stochastic data generation (SDG) to enhance GANs' approximation ability. Our approach is based on the simple idea of imposing randomness through data generation in GANs by a prior distribution on the conditional probability between the layers. Our approach can be easily implemented by using the reparameterization trick. The experimental results on synthetic dataset verify the improved approximation ability obtained by this SDG approach. In the practical dataset, the NSGAN/WGANGP with SDG can also outperform traditional GANs with little change in the model architectures.