Towards Establishing Guaranteed Error for Learned Database Operations
Paper and Code
Nov 09, 2024
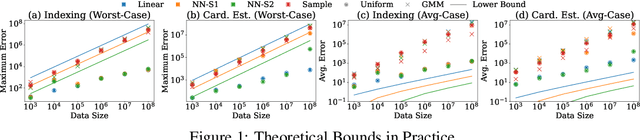
Machine learning models have demonstrated substantial performance enhancements over non-learned alternatives in various fundamental data management operations, including indexing (locating items in an array), cardinality estimation (estimating the number of matching records in a database), and range-sum estimation (estimating aggregate attribute values for query-matched records). However, real-world systems frequently favor less efficient non-learned methods due to their ability to offer (worst-case) error guarantees - an aspect where learned approaches often fall short. The primary objective of these guarantees is to ensure system reliability, ensuring that the chosen approach consistently delivers the desired level of accuracy across all databases. In this paper, we embark on the first theoretical study of such guarantees for learned methods, presenting the necessary conditions for such guarantees to hold when using machine learning to perform indexing, cardinality estimation and range-sum estimation. Specifically, we present the first known lower bounds on the model size required to achieve the desired accuracy for these three key database operations. Our results bound the required model size for given average and worst-case errors in performing database operations, serving as the first theoretical guidelines governing how model size must change based on data size to be able to guarantee an accuracy level. More broadly, our established guarantees pave the way for the broader adoption and integration of learned models into real-world systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge