Towards Better Generalization with Flexible Representation of Multi-Module Graph Neural Networks
Paper and Code
Sep 14, 2022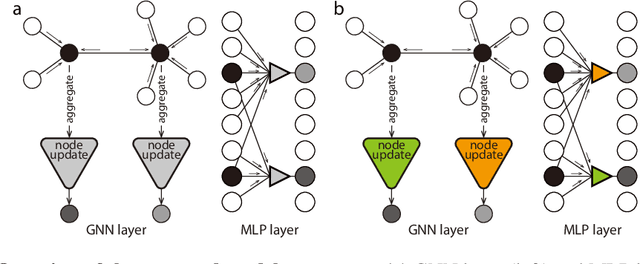

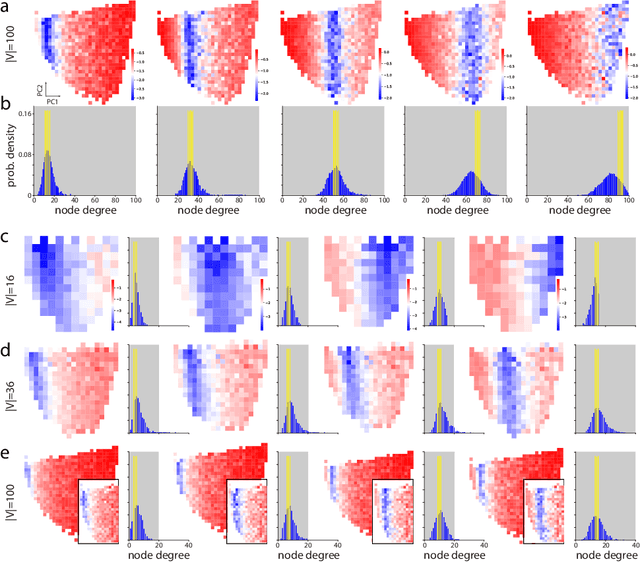
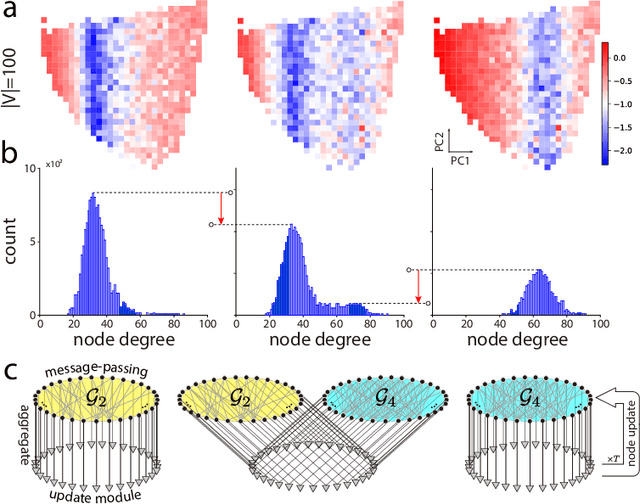
Graph neural networks (GNNs) have become compelling models designed to perform learning and inference on graph-structured data, but little work has been done on understanding the fundamental limitations of GNNs to be scalable to larger graphs and generalized to out-of-distribution inputs. In this paper, we use a random graph generator that allows us to systematically investigate how the graph size and structural properties affect the predictive performance of GNNs. We present specific evidence that, among the many graph properties, the mean and modality of the node degree distribution are the key features that determine whether GNNs can generalize to unseen graphs. Accordingly, we propose flexible GNNs (Flex-GNNs), using multiple node update functions and the inner loop optimization as a generalization to the single type of canonical nonlinear transformation over aggregated inputs, allowing the network to adapt flexibly to new graphs. The Flex-GNN framework improves the generalization out of the training set on several inference tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge