Towards a Better Understanding of Predict and Count Models
Paper and Code
Nov 06, 2015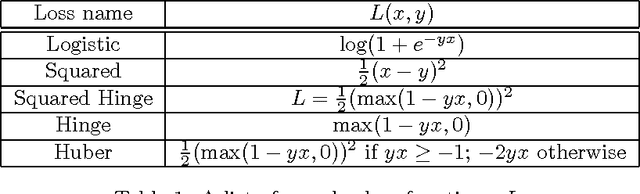
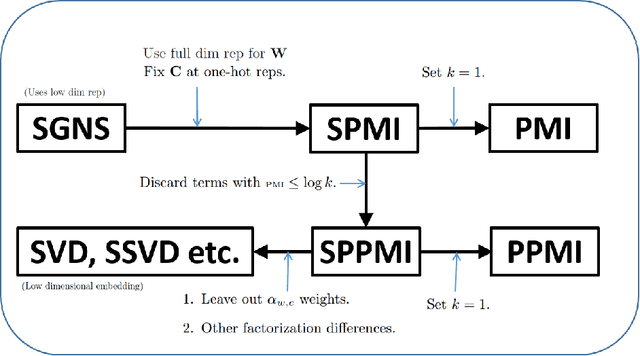
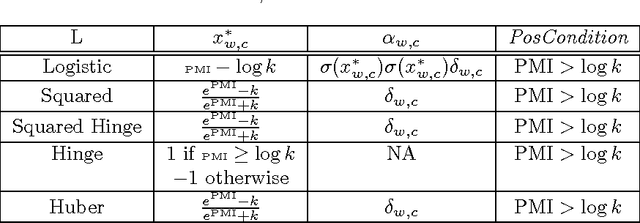
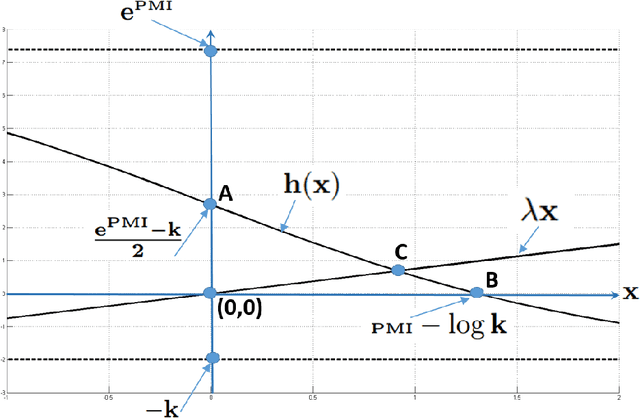
In a recent paper, Levy and Goldberg pointed out an interesting connection between prediction-based word embedding models and count models based on pointwise mutual information. Under certain conditions, they showed that both models end up optimizing equivalent objective functions. This paper explores this connection in more detail and lays out the factors leading to differences between these models. We find that the most relevant differences from an optimization perspective are (i) predict models work in a low dimensional space where embedding vectors can interact heavily; (ii) since predict models have fewer parameters, they are less prone to overfitting. Motivated by the insight of our analysis, we show how count models can be regularized in a principled manner and provide closed-form solutions for L1 and L2 regularization. Finally, we propose a new embedding model with a convex objective and the additional benefit of being intelligible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge