Toward Optimal Feature Selection in Naive Bayes for Text Categorization
Paper and Code
Feb 09, 2016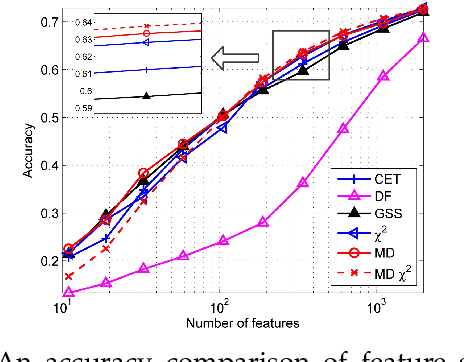
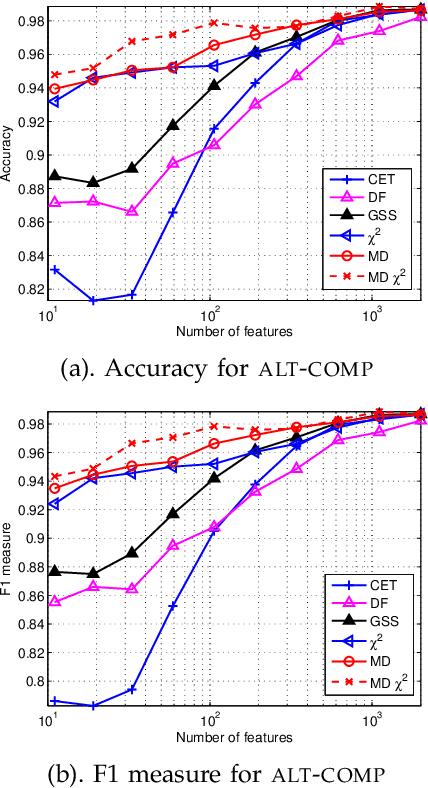
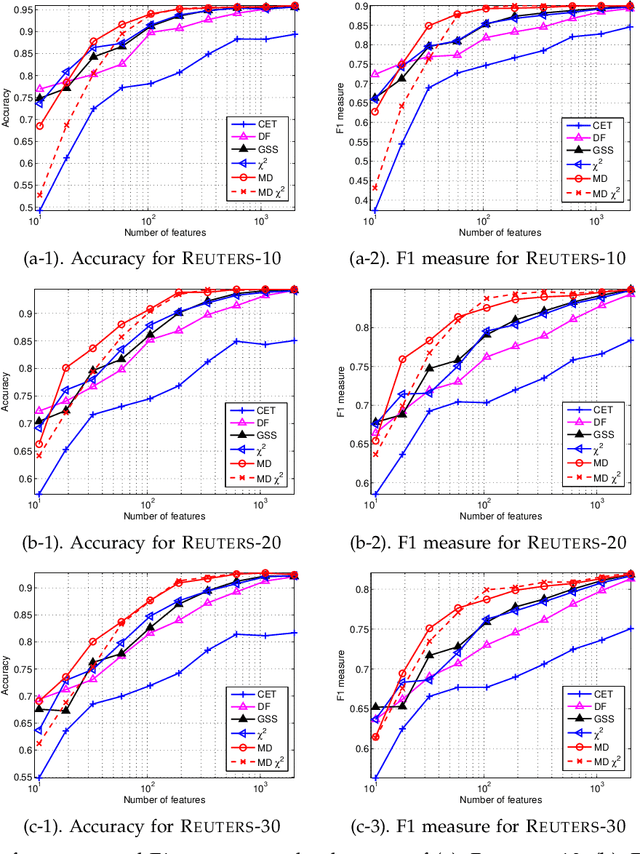
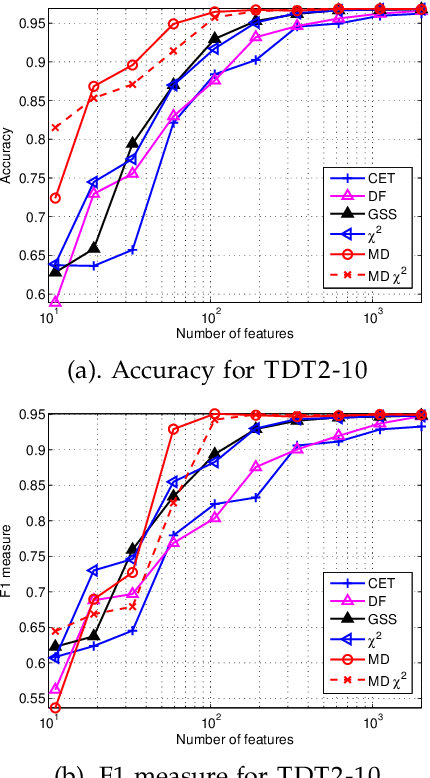
Automated feature selection is important for text categorization to reduce the feature size and to speed up the learning process of classifiers. In this paper, we present a novel and efficient feature selection framework based on the Information Theory, which aims to rank the features with their discriminative capacity for classification. We first revisit two information measures: Kullback-Leibler divergence and Jeffreys divergence for binary hypothesis testing, and analyze their asymptotic properties relating to type I and type II errors of a Bayesian classifier. We then introduce a new divergence measure, called Jeffreys-Multi-Hypothesis (JMH) divergence, to measure multi-distribution divergence for multi-class classification. Based on the JMH-divergence, we develop two efficient feature selection methods, termed maximum discrimination ($MD$) and $MD-\chi^2$ methods, for text categorization. The promising results of extensive experiments demonstrate the effectiveness of the proposed approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge