TopoTune : A Framework for Generalized Combinatorial Complex Neural Networks
Paper and Code
Oct 09, 2024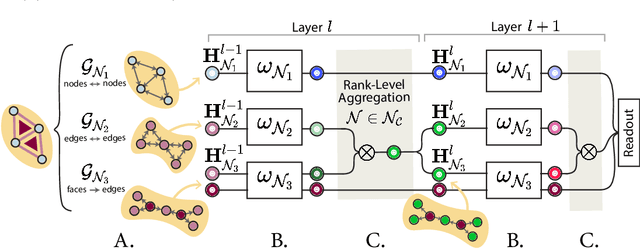
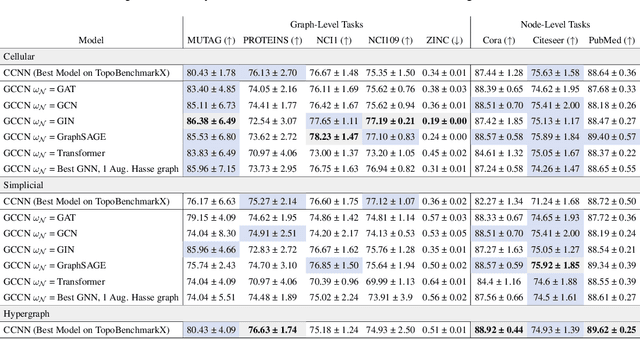
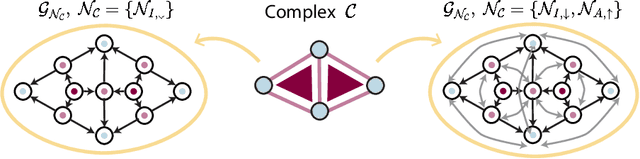
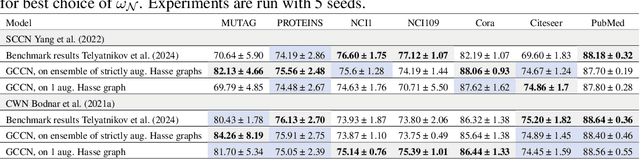
Graph Neural Networks (GNNs) excel in learning from relational datasets, processing node and edge features in a way that preserves the symmetries of the graph domain. However, many complex systems--such as biological or social networks--involve multiway complex interactions that are more naturally represented by higher-order topological spaces. The emerging field of Topological Deep Learning (TDL) aims to accommodate and leverage these higher-order structures. Combinatorial Complex Neural Networks (CCNNs), fairly general TDL models, have been shown to be more expressive and better performing than GNNs. However, differently from the graph deep learning ecosystem, TDL lacks a principled and standardized framework for easily defining new architectures, restricting its accessibility and applicability. To address this issue, we introduce Generalized CCNNs (GCCNs), a novel simple yet powerful family of TDL models that can be used to systematically transform any (graph) neural network into its TDL counterpart. We prove that GCCNs generalize and subsume CCNNs, while extensive experiments on a diverse class of GCCNs show that these architectures consistently match or outperform CCNNs, often with less model complexity. In an effort to accelerate and democratize TDL, we introduce TopoTune, a lightweight software that allows practitioners to define, build, and train GCCNs with unprecedented flexibility and ease.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge