To tune or not to tune the number of trees in random forest?
Paper and Code
May 16, 2017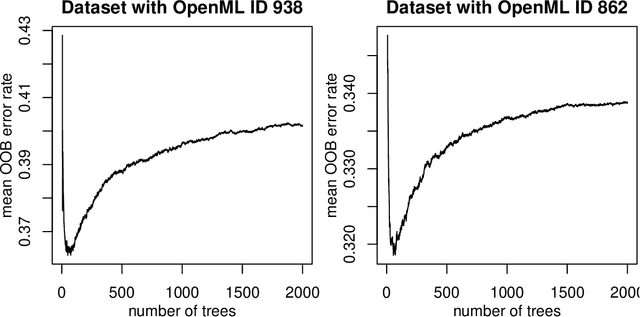
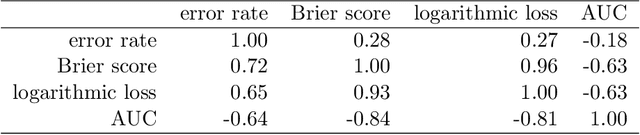
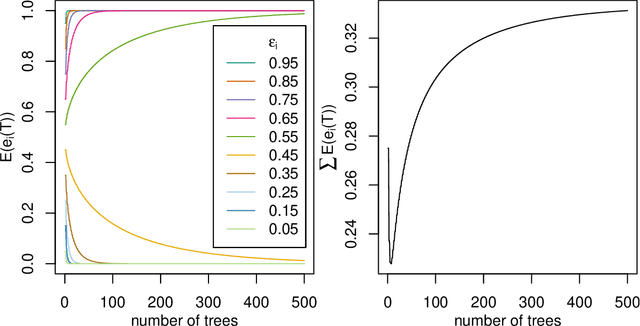
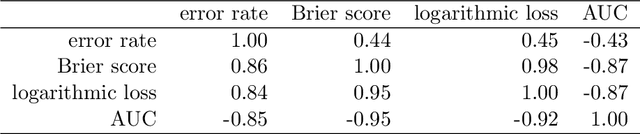
The number of trees T in the random forest (RF) algorithm for supervised learning has to be set by the user. It is controversial whether T should simply be set to the largest computationally manageable value or whether a smaller T may in some cases be better. While the principle underlying bagging is that "more trees are better", in practice the classification error rate sometimes reaches a minimum before increasing again for increasing number of trees. The goal of this paper is four-fold: (i) providing theoretical results showing that the expected error rate may be a non-monotonous function of the number of trees and explaining under which circumstances this happens; (ii) providing theoretical results showing that such non-monotonous patterns cannot be observed for other performance measures such as the Brier score and the logarithmic loss (for classification) and the mean squared error (for regression); (iii) illustrating the extent of the problem through an application to a large number (n = 306) of datasets from the public database OpenML; (iv) finally arguing in favor of setting it to a computationally feasible large number, depending on convergence properties of the desired performance measure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge