Time Series Featurization via Topological Data Analysis: an Application to Cryptocurrency Trend Forecasting
Paper and Code
Dec 07, 2018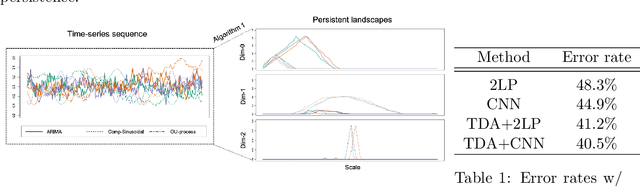
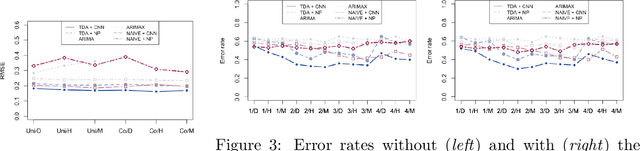
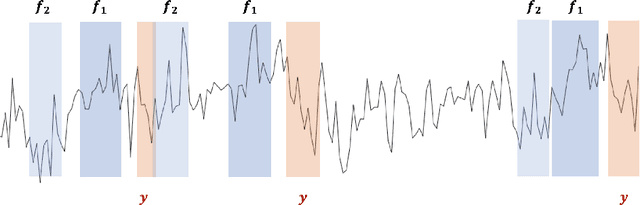
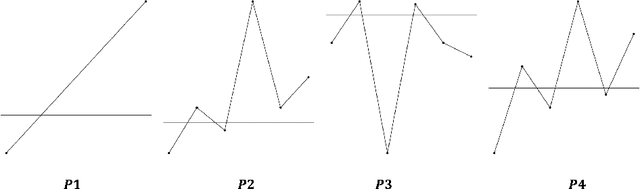
We propose a novel methodology for feature extraction from time series data based on topological data analysis. The proposed procedure applies a dimensionality reduction technique via principal component analysis to the point cloud of the Takens' embedding from the observed time series and then evaluates the persistence landscape and silhouettes based on the corresponding Rips complex. We define a new notion of Rips distance function that is especially suited for persistence homologies built on Rips complexes and prove stability theorems for it. We use these results to demonstrate in turn some stability properties of the topological features extracted using our procedure with respect to additive noise and sampling. We further apply our method to the problem of trend forecasting for cryptocurrency prices, where we manage to achieve significantly lower error rates than more standard, non TDA-based methodologies in complex pattern classification tasks. We expect our method to provide a new insight on feature engineering for granular, noisy time series data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge