Time Series Analysis via Matrix Estimation

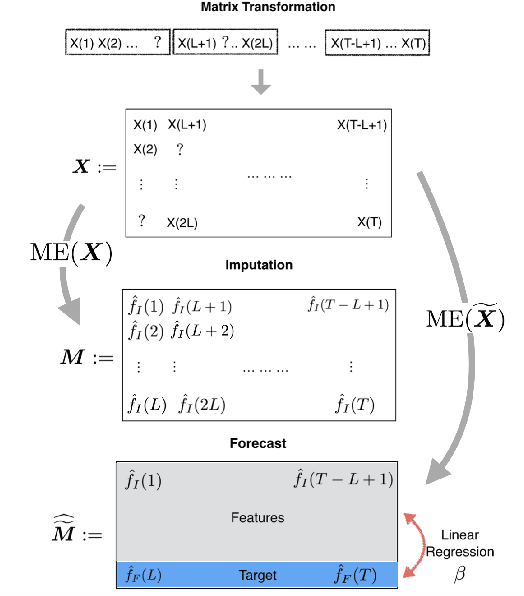
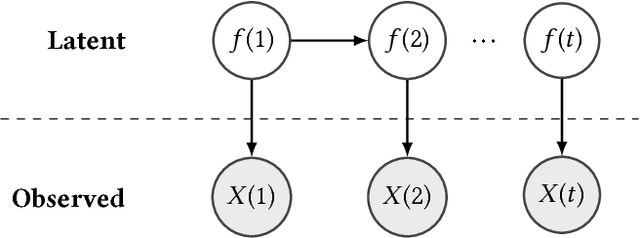
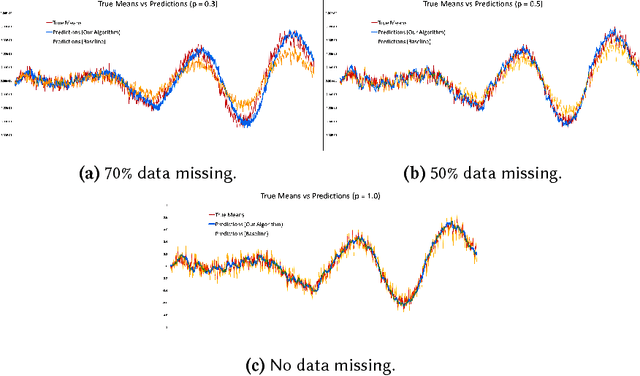
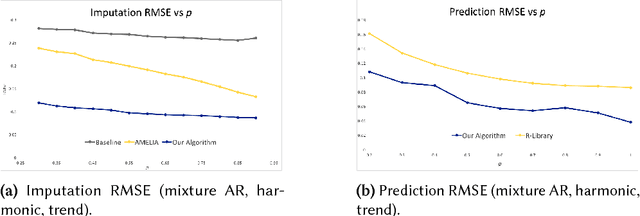
We propose an algorithm to impute and forecast a time series by transforming the observed time series into a matrix, utilizing matrix estimation to recover missing values and de-noise observed entries, and performing linear regression to make predictions. At the core of our analysis is a representation result, which states that for a large model class, the transformed matrix obtained from the time series via our algorithm is (approximately) low-rank. This, in effect, generalizes the widely used Singular Spectrum Analysis (SSA) in literature, and allows us to establish a rigorous link between time series analysis and matrix estimation. The key is to construct a matrix with non-overlapping entries rather than with the Hankel matrix as done in the literature, including in SSA. We provide finite sample analysis for imputation and prediction leading to the asymptotic consistency of our method. A salient feature of our algorithm is that it is model agnostic both with respect to the underlying time dynamics as well as the noise model in the observations. Being noise agnostic makes our algorithm applicable to the setting where the state is hidden and we only have access to its noisy observations a la a Hidden Markov Model, e.g., observing a Poisson process with a time-varying parameter without knowing that the process is Poisson, but still recovering the time-varying parameter accurately. As part of the forecasting algorithm, an important task is to perform regression with noisy observations of the features a la an error- in-variable regression. In essence, our approach suggests a matrix estimation based method for such a setting, which could be of interest in its own right. Through synthetic and real-world datasets, we demonstrate that our algorithm outperforms standard software packages (including R libraries) in the presence of missing data as well as high levels of noise.