Time-Optimal Trajectory Planning in Highway Scenarios using Basis-Spline Parameterization
Paper and Code
Oct 05, 2023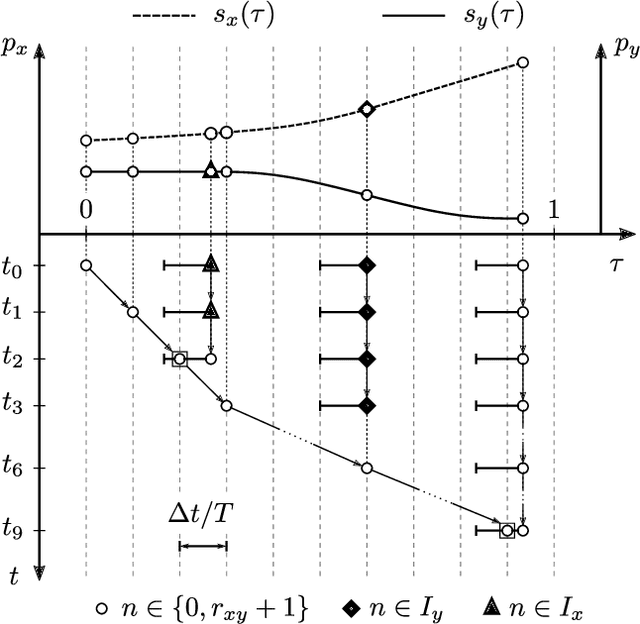
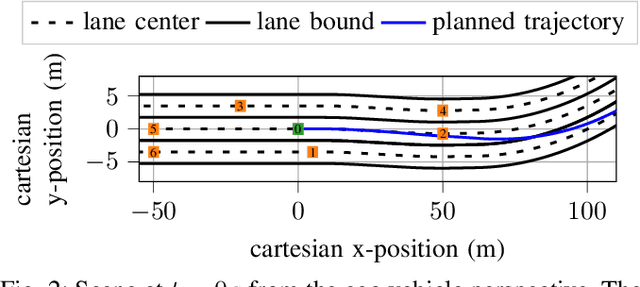
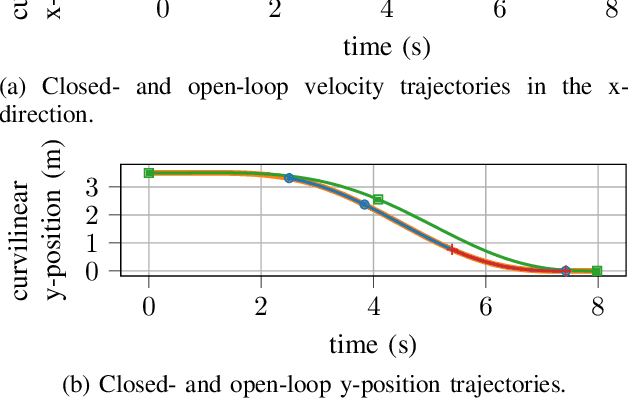
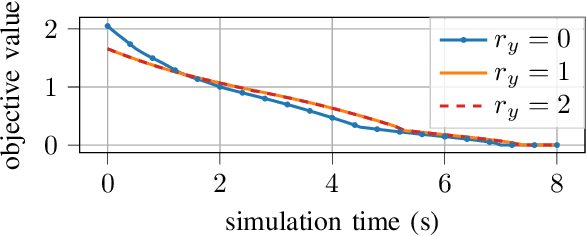
Basis splines enable a time-continuous feasibility check with a finite number of constraints. Constraints apply to the whole trajectory for motion planning applications that require a collision-free and dynamically feasible trajectory. Existing motion planners that rely on gradient-based optimization apply time scaling to implement a shrinking planning horizon. They neither guarantee a recursively feasible trajectory nor enable reaching two terminal manifold parts at different time scales. This paper proposes a nonlinear optimization problem that addresses the drawbacks of existing approaches. Therefore, the spline breakpoints are included in the optimization variables. Transformations between spline bases are implemented so a sparse problem formulation is achieved. A strategy for breakpoint removal enables the convergence into a terminal manifold. The evaluation in an overtaking scenario shows the influence of the breakpoint number on the solution quality and the time required for optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge