Time-optimal Coordination of Mobile Robots along Specified Paths
Paper and Code
Apr 05, 2017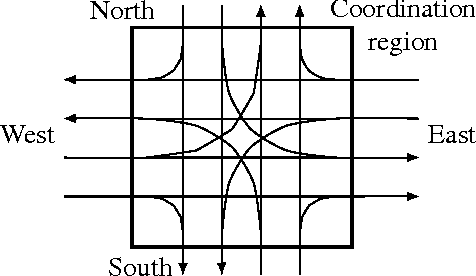
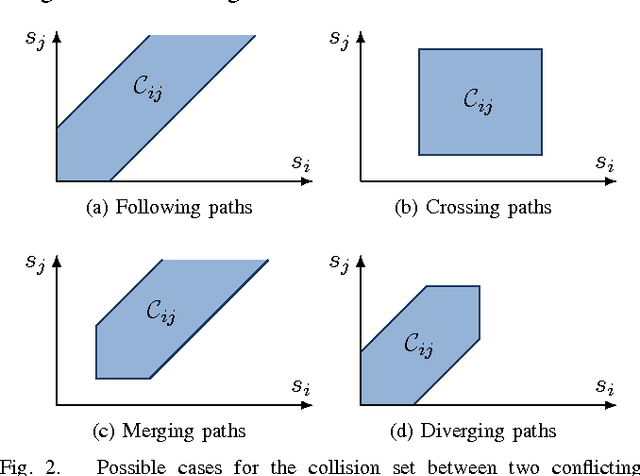
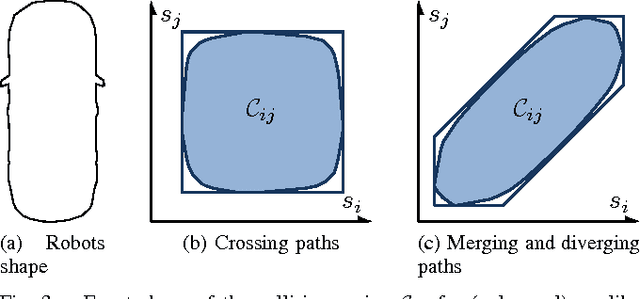
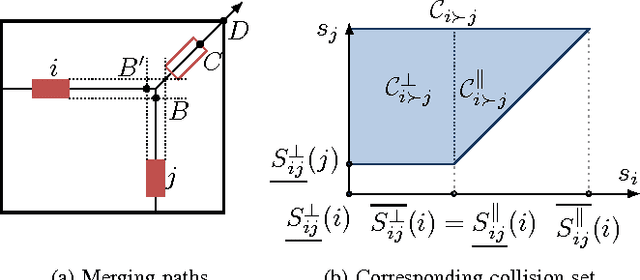
In this paper, we address the problem of time-optimal coordination of mobile robots under kinodynamic constraints along specified paths. We propose a novel approach based on time discretization that leads to a mixed-integer linear programming (MILP) formulation. This problem can be solved using general-purpose MILP solvers in a reasonable time, resulting in a resolution-optimal solution. Moreover, unlike previous work found in the literature, our formulation allows an exact linear modeling (up to the discretization resolution) of second-order dynamic constraints. Extensive simulations are performed to demonstrate the effectiveness of our approach.
* Published in 2016 IEEE/RSJ International Conference on Intelligent
Robots and Systems (IROS)
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge