TILDE-Q: A Transformation Invariant Loss Function for Time-Series Forecasting

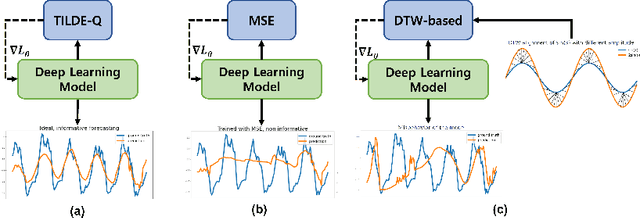
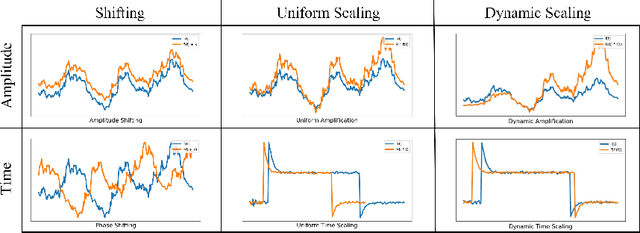
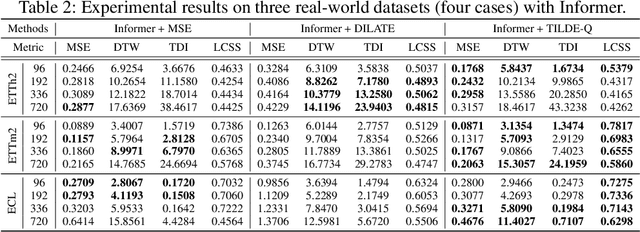
Time-series forecasting has caught increasing attention in the AI research field due to its importance in solving real-world problems across different domains, such as energy, weather, traffic, and economy. As shown in various types of data, it has been a must-see issue to deal with drastic changes, temporal patterns, and shapes in sequential data that previous models are weak in prediction. This is because most cases in time-series forecasting aim to minimize $L_p$ norm distances as loss functions, such as mean absolute error (MAE) or mean square error (MSE). These loss functions are vulnerable to not only considering temporal dynamics modeling but also capturing the shape of signals. In addition, these functions often make models misbehave and return uncorrelated results to the original time-series. To become an effective loss function, it has to be invariant to the set of distortions between two time-series data instead of just comparing exact values. In this paper, we propose a novel loss function, called TILDE-Q (Transformation Invariant Loss function with Distance EQuilibrium), that not only considers the distortions in amplitude and phase but also allows models to capture the shape of time-series sequences. In addition, TILDE-Q supports modeling periodic and non-periodic temporal dynamics at the same time. We evaluate the effectiveness of TILDE-Q by conducting extensive experiments with respect to periodic and non-periodic conditions of data, from naive models to state-of-the-art models. The experiment results indicate that the models trained with TILDE-Q outperform those trained with other training metrics (e.g., MSE, dynamic time warping (DTW), temporal distortion index (TDI), and longest common subsequence (LCSS)).