Tighter Variational Bounds are Not Necessarily Better. A Research Report on Implementation, Ablation Study, and Extensions
Paper and Code
Sep 23, 2022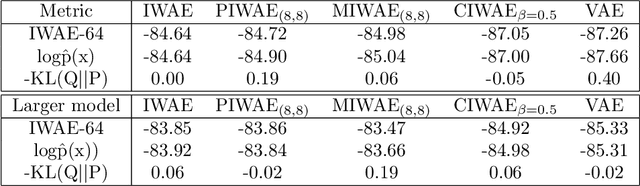
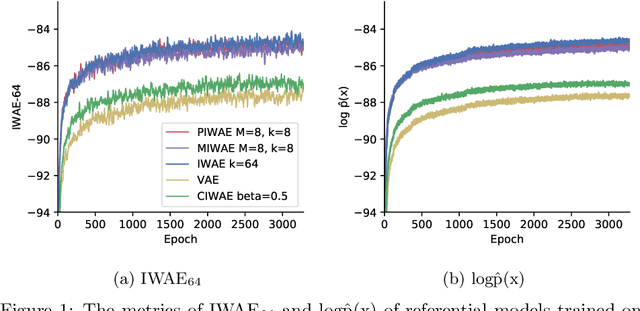
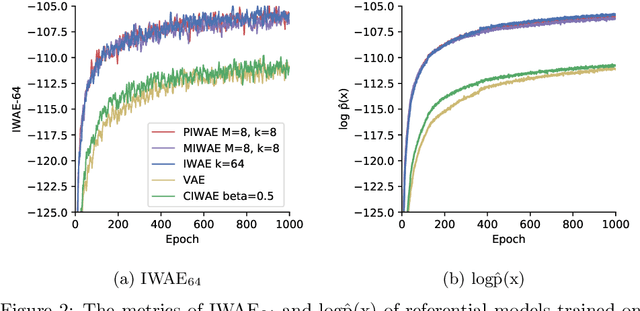

This report explains, implements and extends the works presented in "Tighter Variational Bounds are Not Necessarily Better" (T Rainforth et al., 2018). We provide theoretical and empirical evidence that increasing the number of importance samples $K$ in the importance weighted autoencoder (IWAE) (Burda et al., 2016) degrades the signal-to-noise ratio (SNR) of the gradient estimator in the inference network and thereby affecting the full learning process. In other words, even though increasing $K$ decreases the standard deviation of the gradients, it also reduces the magnitude of the true gradient faster, thereby increasing the relative variance of the gradient updates. Extensive experiments are performed to understand the importance of $K$. These experiments suggest that tighter variational bounds are beneficial for the generative network, whereas looser bounds are preferable for the inference network. With these insights, three methods are implemented and studied: the partially importance weighted autoencoder (PIWAE), the multiply importance weighted autoencoder (MIWAE) and the combination importance weighted autoencoder (CIWAE). Each of these three methods entails IWAE as a special case but employs the importance weights in different ways to ensure a higher SNR of the gradient estimators. In our research study and analysis, the efficacy of these algorithms is tested on multiple datasets such as MNIST and Omniglot. Finally, we demonstrate that the three presented IWAE variations are able to generate approximate posterior distributions that are much closer to the true posterior distribution than for the IWAE, while matching the performance of the IWAE generative network or potentially outperforming it in the case of PIWAE.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge