Tightening Discretization-based MILP Models for the Pooling Problem using Upper Bounds on Bilinear Terms
Paper and Code
Jul 08, 2022
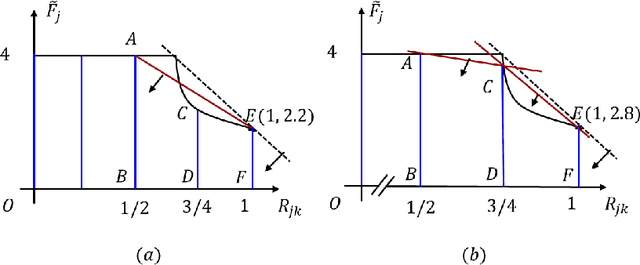
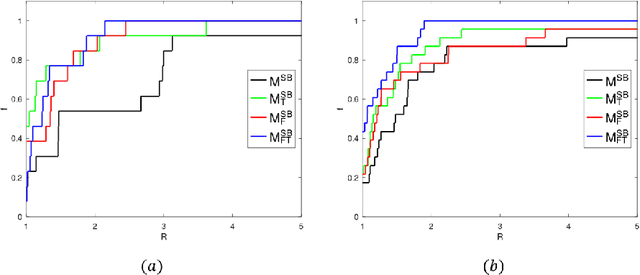
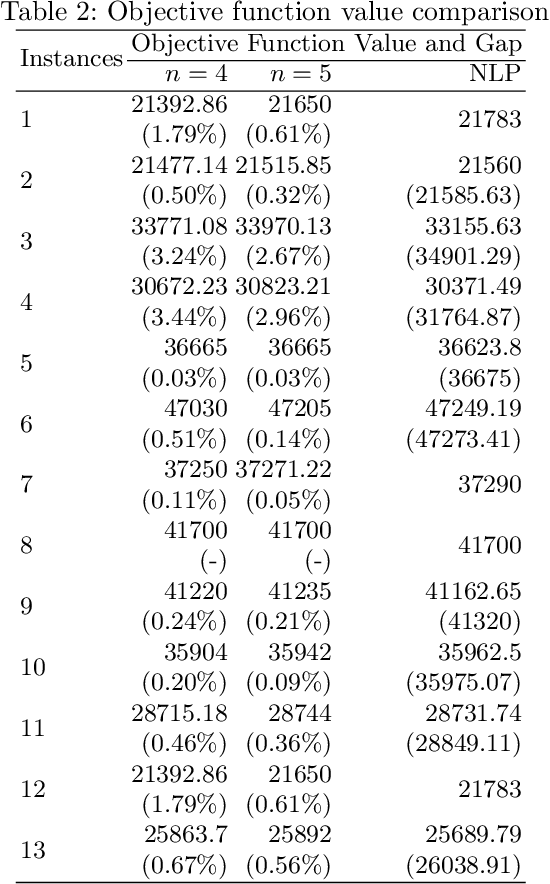
Discretization-based methods have been proposed for solving nonconvex optimization problems with bilinear terms. These methods convert the original nonconvex optimization problems into mixed-integer linear programs (MILPs). Compared to a wide range of studies related to methods to convert nonconvex optimization problems into MILPs, research on tightening the resulting MILP models is limited. In this paper, we present tightening constraints for the discretization-based MILP models for the pooling problem. Specifically, we study tightening constraints derived from upper bounds on bilinear term and exploiting the structures resulting from the discretization. We demonstrate the effectiveness of our constraints, showing computational results for MILP models derived from different formulations for (1) the pooling problem and (2) discretization-based pooling models. Computational results show that our methods reduce the computational time for MILP models on CPLEX 12.10. Finally, we note that while our methods are presented in the context of the pooling problem, they can be extended to address other nonconvex optimization problems with upper bounds on bilinear terms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge